定量的な推測をする為の情報
***以下の記述は、とっても簡略化されていたり、(対象とする人たちに)分かりやすいと思われる形にした(つもり)なので、専門家や学者さんが読んでしまった場合は、あんまり怒らないで下さいね。一応、酷く間違ったことは言ってないと思いますが、勘違いや間違いをしている点などはご指摘頂ければ、幸いです。***
- 一部で、計算間違いをしていたので、直しました。小学生の計算を間違えていました・・・
私は、素人測定に於いて、無理に定量的な推測をする必要はないだろうと思っています。
それは、素人測定で使われる機材の感度が限られており、たとえ、3インチの検出器を
入手しても、簡単に1Bq/kg未満の領域が見えるわけでもなく、それ以下の大きさの結晶ならば、
自分の測定器で山が見えたら、それは、もうある程度の危険と同じと考えても良いと思うからです。
もちろん、10Bq/kgくらいの濃度まで、あるいは、100Bq/kgくらいまでは食べちゃおう、
という人などは、1インチのアルマジロで、十分自分なりの決定を下せるわけですが、
ゼロにすることが出来ないのは承知でも、出来るだけ放射性汚染物質は食べたくない、という場合、
1Bq/kgはおろか、それ以下でも食べたくないわけですから、自分の測定器で、
怪しいと思ったら、食べるのを躊躇いますし、山がはっきりしてたら、それは、もう食べないでしょうから。
しかし、色々な理由で、定量的な推測をしたい場合は、簡単な原理を理解していると、
変な思い込みにとらわれてしまったりする可能性が低くなります。
定量的な推測の原理
- 1Bqの放射性物質は、おおよそ、1秒に1回くらい崩壊する。
ただし、その間隔は、バラバラで、規則性が無いと言われています。
ところが、崩壊を観測し続けると、その間隔の平均は、徐々に落ち着いて、
1秒に1回くらいの割合に近づいていくわけです。
従って、「沢山観測しないと、ばらついていて良く分からない」のが放射能測定です。
100回、千回、一万回と回数が増えるに連れ、より正確になっていきます。
ともかく、1Bqは「毎秒1回の崩壊」ということで、
Bq(ベクレル)という放射能の単位は、「毎秒の崩壊数」
という点が大事です
- 測定器は、おおよそ決まった割合で、この崩壊を計測する。
測定器には、様々な種類がありますが、
セシウム137の様な核種の崩壊を観測できる割合(効率)が
それぞれ、おおよそ決まっています。
例えばセシウム137の「ピークの部分について」考えると、
ある測定器では、100回の崩壊に付き5回を観測できる、
というようなことが計算や実測から分かります。
1Bqは「毎秒の崩壊数」で、その5%を測定器がピークとして捉えるとすると
ピークの部分の「毎秒のカウント数」は、0.05cps (カウント・パー・セコンド)となります。
なので、測定した結果、ピークの部分の「毎秒のカウント数(計数率)」が、0.05cps ならば
検体には1Bqの放射能がある、と言えます。
つまり、この例では、Cs137のピーク部分の「毎秒のカウント数(計数率)」に100÷5=20で
20をかけると、その検体の中のセシウム137の放射能が計算できます。
- 既にどれだけの放射性物質を含んでいるのが、おおよそ分かっている検体を計測すると、上記の「割合」が分かる。
たとえば、10Bq/kgの濃度のセシウム137が含まれる検体が1kgあれば、
検体内の中に、10Bqのセシウム137を含んでいます。
(測定器にとっては、検体の中の放射性物質の総量が大事。)
これを測り、セシウム137のピークのカウント数を測定秒数で割って「毎秒のカウント数(計数率)」にします。
たとえば、10時間(60秒 x 60分 x 10時間 = 36000秒)測って、Cs137のピークの部分の
カウント数が1800回あったとすると、ピークの計数率(レート)は、
1800(counts、回) ÷ 36000(seconds、秒) = 0.05(cps, counts per minute、回/秒)
その計数率で10Bqを割れば、ピークの計数率と検体に含まれるセシウム137の割合が分かります。
ピークの計数率が0.05cpsなら、10Bq / 0.05cps = 20Bq/cps
- 割合が分かったら、調べたい検体を「同じ条件」で測って、ピークの計数率に、この割合を掛け合わせれば良いだけ。
先ほどの例の様に、20Bq/cpsの割合だと分かったら、調べたい検体を測定して、
ピークの部分のカウント数を調べて、測定秒数で割って、
それに20Bq/cpsをかけると、その検体の中のセシウム137の総量がおおよそ分かります。
で、それを検体の重さ(kg)で割れば、単位重量あたりの濃度(Bq/kg)が計算できます。
例えば、検体のピークが合計で9000カウントあり、36000秒測ったのだとしたら、ピークの計数率は、
900(counts、回) ÷ 36000(seconds、秒) = 0.025 (cps, counts per minute、回/秒)
それに、20Bq/cpsをかけると、
0.025(cps) × 20(Bq/cps) = 5(Bq)
もし、検体の重量が800グラムなら、0.8kgなので、
5(Bq) / 0.8(kg) = 6.26(Bq/kg)
ということになります。
要は、多くの人が考えているよりもかなり簡単なのですが、本当に「正確に測ろう」とすると色々と難しくなります。
- では、どうやって、ピークの部分のカウント数や計数率を出すのか?
昔昔から、色々な方法が考えられていて、ピークが本当にくっきりと出ている場合には、
ピークの根元の位置を適当に判断して、その位置(カウント数か計数率)よりも上の部分を
数えれば良いわけです。
ただ、これを該当するチャンネルについて、一々手作業でやると面倒なので、
普通は、ソフトがやってくれます。
テレミノMCAの作業中の版では、マーカーを出す要領でピークの根元の中心と思われる位置で
マウスを右クリックすると、ピーク情報が出てきて、その根元から、ピークの先端までの高さや、
FWHMやピークの中央を推測し、それに合致するガウス曲線を描いて、その計数率(面積)などを
表示しますので、後は、その計数率に換算係数をかけて、何ベクレルに相当するのか出し、
それを検体の重量(kg)で割れば、単位重量当たりの濃度(Bq/kg)が出ます。
自分でやりたい場合には、エクセルとか、Gnuplotとか、Rとか、まあ、
数表なり数値を扱えるソフトで、色々なやり方で計算できます。
でも、もっと簡単な方法もあります。
- ピークの部分の計数率と、ピークの高さは比例している。
つまり、ピークの部分のカウント数の合計(俗に「面積」と言ったりしますが)を計算しなくても、
ピークの高さと放射能の割合を調べておけば、ピークの高さを測るだけで、「定量的な推測」が
出来るわけです。
この場合、単純に、ピークの高さと検体内に含まれる放射能の比例関係を線量の分かっている線源から割り出し、
後は、この係数を検体のピークの高さにかけるだけ、という方法でも良いでしょう。
例えば、20Bqのセシウム137を含む線源があって、セシウム137のピークが(根元から)0.04cpsの高さだったなら、
20Bq/0.04cps = 500Bq/cps となります。
で、「同じ条件」で検体のスペクトルを取って、セシウム137のピークが0.02cpsの高さだったら、
0.02cps x 500Bq/cps = 10Bq となります。
(まあ、この場合は、単純に半分の高さだから1/2の放射能だと分かりますが)
チャンネル数の配分(チャンネルピッチ)を変えたり、横軸の校正が大きくずれたりしたら、
この割合も変わってしまうので、再度線源を測って換算係数を出しなおすことになります。
ただし、この様にピークの高さを使う場合には、ピークのカウント数が大きくなって、ピークが丸く滑らかになってからでないと
ばらつきが大きくなるので、ギザギザでグチャグチャのスペクトルでもって数値を得ようとしている場合などは、注意が必要です。
また、根元がどこか?という点もきちんと考えて注意しないと、結果の信頼性がどんどん下がります。
そして、ピークがその左右よりもはっきりと盛り上がっているのでないなら、この方法でも、
あるいは、どんな方法でも、多少なりとも信頼できるような結果は得られません。
スペクトルがグチャグチャだということは、測定環境の安定性が極端に悪いのか、
カウント数が非常に少なくて、ばらつきが大き過ぎて、非常に不確かな状態だと言う事です。
そういう状態だと、「はっきりと言える事」は少なくなり、そういう測定に基づいて色々考えても
あまり意味のある解釈には辿り着けないでしょう。
高さを使うのと面積を使うことに関しては、このページなどにも書かれています。
- ピークの高さとピークの面積は単純に比例している
ピークの形は、ガウス曲線というカーブに良く似てくることが知られていて、この曲線の面積が
ピークのカウント数、又は計数率とほぼ一致します。
ガウス曲線の面積は、その高さと、測定器のそのエネルギー位置での分解能、そして、
全体の何パーセントの部分まで含めるか、という幅の設定で決まります。
ガウス曲線の性質を使って、
スペクトルのピークの高さから、その面積を求めたい場合は、以下の式で計算できます。
高さ(cps) x ピークの中央のチャンネル番号 x FWHM(%)/100 x 1.064467 = 面積(ピークの計数率、レート、cps)
例えば、分解能がセシウム137のエネルギー位置で9%の測定器の場合、
662keVが323チャンネルだったら、FWHMは、323(ch) x 0.09 (9%) = 29.07(ch)
従って、ピークの高さが1cpsの計数率なら面積は、
1 x 29.07 x 1.064467 = 30.94404(cps)
となります。
この場合、Cs137については、山の高さを約31倍すると面積が出ることになります。
上の方法の考え方(詳しく知りたい場合)
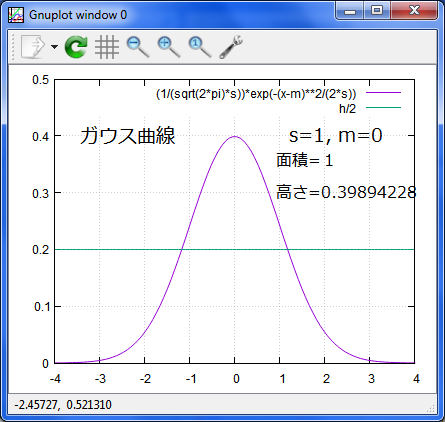
ガウス曲線は、統計の正規分布でも良く使われ、その場合は、
面積の合計が確率の「全ての場合」に相当する1になる形の式で説明されています。
ピークの高さは、1/√(2π)で、0.3989・・・になり、約0.4です。

ピークの面積を求める場合、常に面積が1では困るわけですし、高さを基準にしたいので、
上の式の左側の1/√(2π)σを取ってしまいます。
すると、このガウス関数の全域の面積は、単純に、高さとσ(シグマ)に比例することになり、
面積 = 高さ x √(2π) x σ
となります。
√(2π)は、円周率の2倍の平方根で、2.506628 です。
また、σ(シグマ)は、
σ(シグマ) = FWHM(チャンネル幅) ÷ 2√(2ln2) = FWHM(チャンネル幅) ÷ 2.35482
で、さらに、
FWHM(チャンネル幅) = ピークの中央のチャンネル番号 x FWHM(%)/100
なので、これらを組み合わせると
面積 = 高さ x √(2π) x (ピークの中央のチャンネル番号 x FWHM(%)/100) ÷ 2√(2ln2)
となり、√(2π) ÷ 2√(2ln2) = 1.064467なので、
面積 = 高さ x (ピークの中央のチャンネル番号 x FWHM(%)/100) x 1.064467
という風にまとられます。
要は、FWHMの数値(%)を該当するピークのチャンネル番号にかけて、
チャンネル数でのFWHMの値を求め、それと高さと 1.064467 をかければ面積が計算出来るわけです。
FWHMの値も、そのチャンネル番号(Bin)もテレミノMCAのマーカーで直ぐに分かりますし、
他のソフトでも大抵似た様な機能が付いています。
もっと「おおよそ」の計算で良いなら、1.064467は、1と等しいとみなして無視し、
面積 = 高さ x (ピークの中央のチャンネル番号 x FWHM(%)/100)
と考えても良いでしょう。
この場合、面積は6%程度小さく値に計算されますので、他の計算方法やソフトと比較、照合する場合には、
その点を忘れない方が良いでしょう。
ピークの高さや面積を計数率(cps)で計算する場合が多いですがカウント数で計算しても構いません。
上記の計算は、ピーク面積の全体を想定した場合の話ですので、ROIを狭く取ってしまったりするなら、
統計で言うところの信頼区間の確率に相当する割合で、面積は小さくなり、その場合、
ROIの幅が(片側で)何σ(シグマ)なのか調べ、その値に相当する信頼区間に確率の数字を
全面積にかければ、そのROIの幅のピークの面積が推測できます。
2σ(シグマ)で約95%、3σ(シグマ)で約99.7%ですから、3σもあれば、素人測定の精度では
「ピーク全体」として見なして問題ありません。
自分で確かめたい、考えたい場合などは、以下の様なページが参考になるかも。
http://www.eng.kagawa-u.ac.jp/~tishii/Lab/Etc/gauss.html
http://ja.wikipedia.org/wiki/%E3%82%AC%E3%82%A6%E3%82%B9%E9%96%A2%E6%95%B0
http://d.hatena.ne.jp/Zellij/20130122/p1
http://www.lightstone.co.jp/origin/flist6.html
http://www.nabe-e.com/support/help/calcpkf.htm
小まとめ
- ピークの計数率と検体の中の放射能は、比例している。
- なので、既に放射能の分かっている検体で、測定器固有の割合を求めれば、調べたい検体の放射能も分かる。
- 測っているのは、重量当たりの放射能濃度(Bq/kg)ではなく、検体の中の放射能(Bq)。濃度で考えるのではなく、Bqで考える癖を付けておくと良い。
- 測定の不確かさは、カウント数が増えるほど減る。カウント数が十分あれば、スペクトルは落ち着いてくる。
- ピークの高さとピークの計数率も単純に比例しているので、線量が分かっている線源で線量と高さの割合を調べれば、検体の線量が分かるようになる。
- 高さを使うと手ごろだけど、注意が必要。条件が変わったら、割合も変わる。
- 高さを使う場合、滑らかになったスペクトルか十分にスムージングをかけたスペクトルでないと、信頼性が低くなる。
- カウント数が少なく、グチャグチャのスペクトルは、細かいこと、微妙なことの考察にはほとんど役立たない。
- カウント数が少なくても、汚染が強ければ、ピークが良く見えたり、計算して推測が出来たりする。
- 汚染も微妙で、カウント数が少ない場合、あんまり良く分かりません。むなしい奮闘や単なるロマンの追及は、「測定」には役立ちません。
もう少し詳しい話
計数率(cps)と放射能(Bq)の割合は、数々の条件に左右されます。
その中には、検体の物質の原子番号とか、密度とか、他にも、温度とか色々あるので、
出来るだけそういうものの条件を揃えた方が正確な結果になる筈です。
でも、おそらく一番大きく左右するのが、俗に「ジオメトリー」と呼ばれる、
検体と測定器の位置関係です。
たとえば、自家製や市販のマリネリ容器を使って測る場合、マリネリの輪の部分と、上の方では、
測定器が崩壊を捉える割合が異なります。
なので、違う詰め方をすると、結果が変わります。
少量の検体を量りたい場合、マリネリを縦割りにして、半分、四分の一、といった部分に検体を詰めると、
このジオメトリーの違いによる問題がかなり少なくなります。
マリネリの輪の中と、マリネリの蓋に近いほうでは、感度に数倍以上の差があるかもしれません。
なので、ジオメトリーについては、気を付けた方が良いでしょう。
ただし、元々放射能測定には不確かさが付き物で、ましてや素人測定では、
最初の一桁か二桁があっていたら「大正解」くらいに思っていた方が良いので、
詰め方にムラがあったり、量が少し違っていても、そんなに気にする必要はないでしょう。
そして、その方が、自分の測定を過信するという可能性も低くなるかもしれません。
密度や水分や、その他色々な要因があって、興味があるならWEBに沢山資料や
ソフトがあって、計算することも出来ます。
しかし、どんなに頑張っても、「この世の仕組み」の一つとして、
放射能測定の結果は必ずばらつきます。
そして、ガンマスペクトル測定で、定量的な推測をする場合、
小数点数桁までの正確な値を得られる様なものではないのだ、という点を
忘れない様にすると、「無駄な努力」「空回りする奮闘」「変な思い込みや勘違いの数々」が
少しは減るのではないかと思います。