コンプトン散乱 / コンプトン効果
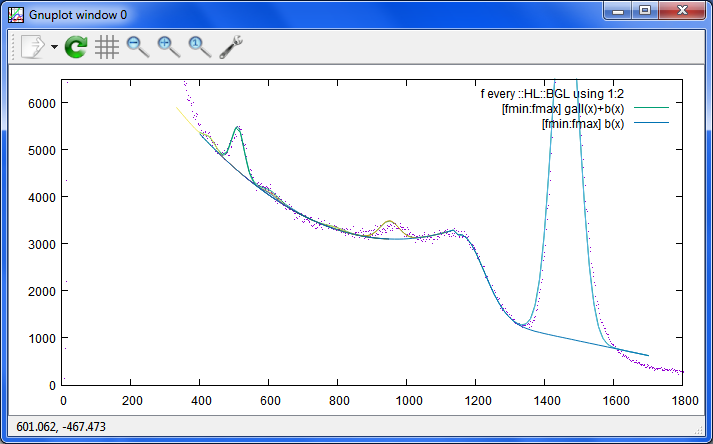
K40のコンプトン散乱によるコンプトンバレーやコンプトンプラトーが顕著に出たスペクトルにGnuplotでフィットした例。
私は、コンプトン効果(散乱)をこんな風に捉えています。
(これは、間違っていたり、表現が適当でないかもしれないので、真面目に勉強をした方や、詳しい方の意見を確かめましょう。)
X線やガンマ線が、物質の中で電子を弾き飛ばして、その結果軌道が変化します。
つまり、ビリヤードで突いた玉が、他の玉に当たって、方向が変わるのと、同じ様なものです。
私たちは、スペクトル上では、この「弾き飛ばされた他の玉(電子)」のエネルギーを
コンプトン散乱として観測します。
光電ピーク = 元のガンマ線のエネルギーを観測
コンプトン散乱 = 弾き飛ばされた電子のエネルギーを観測

ただ、弾き飛ばされた玉に、エネルギーを与えたので、進行方向が変わるだけでなく、エネルギーも低下しますが、
逆に言うと、ガンマ線の進行方向が大きく変わる程(最大180度)、弾き飛ばす電子に与えるエネルギーが大きくなり、
その電子を観測しているコンプトン散乱は、他の玉に衝突せずにそのまま吸収されたガンマ線のピーク
(光電ピーク。全吸収ピークとも言う)に近い位置に現れます。
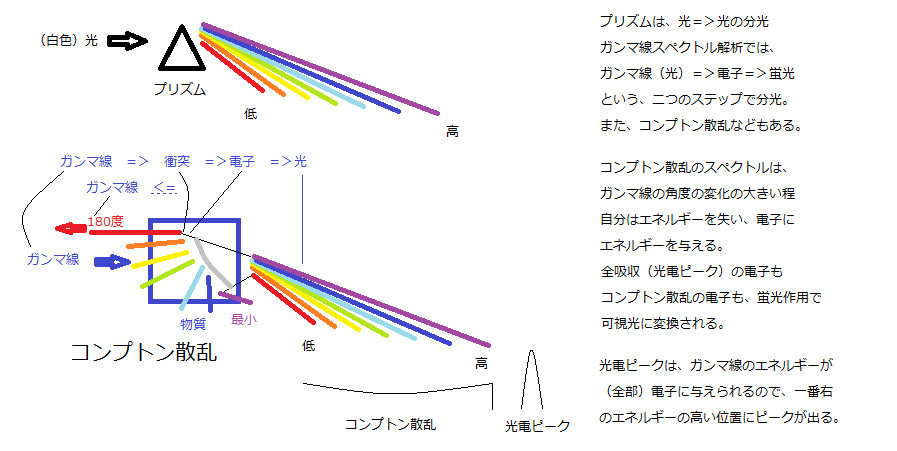
ガンマ線スペクトル分析で、俗にいう「ピーク/山」は、光電ピーク(PhotoPeak)とか
呼ばれたりもしますが、ガンマ線のエネルギーが電子に全吸収されて出るもの。
なので、その電子は、ピチピチしていて波長も短いしエネルギーも高い。
これに対し、コンプトン散乱は、ガンマ線のエネルギーが、ガンマ線が跳ね返る角度によって
電子に与えられるので、一番跳ね返る角度の大きい180度の時、電子が
一番高いエネルギーになるが、跳ね返ったガンマ線の方は一番エネルギーを失う。
跳ね返ったガンマ線は、ほとんどは逃げてしまって、観測されない。
この一番右側(光電ピークに近い立ち上がり)を「コンプトンエッジ」、
これと光電ピークの間のへこみを「コンプトンバレー」と呼びます。
コンプトン散乱の少しへこんだ持ち上がり、丘の様になった高台を
コンプトンプラトーと呼ぶ場合もあります。
全吸収のものも、コンプトン散乱のものも、電子(ベータ線)は、
蛍光作用を引き起こして、そのエネルギーに対応した強さの可視光を出します。
そして、PMT(光電子増倍管、フォトマルチプライヤーチューブ)やPD(フォトダイオード)などは、
その可視光を、電気信号(電子)に変えて、スペクトルとなります。
下の図は、オランダのScinixという検出器メーカーのページからのもので、PhotoPeak(光電ピーク)が662KeVにあり、その左のへこみが、コンプトンバレー。
その左がコンプトンエッジで477KeV。そして、なだらかな窪みのあと、185KeV付近の持ち上がりがバックスキャッターピーク。
バックスキャッターは、測定器とは逆の方へ向かったガンマ線が、遮蔽の中で電子に当たって弾け、
反対方向に飛んで測定器の中で全吸収されたものです。ガンマ線が180度方向を変えた場合、
ガンマ線は、電子に最大のエネルギーを与え、自分はその分のエネルギーをうしなったので、
残っているエネルギーは、全吸収ピークのエネルギーから、コンプトンエッジのエネルギー引いたものになります。
コンプトンバレーは、結晶の大きい検出器では、凹みが埋まってきて、結晶が小さいと、よりはっきりとするようです。
これは、電子を弾き飛ばして跳ね返ったガンマ線が今度は吸収される割合が結晶が大きい程高いからです。
(この図は、バックグラウンドを差し引いた後、または、バックグラウンドが無い状態で測定した場合のスペクトルです。)

http://www.scionix.nl/interaction.htm
以下の計算式などは、興味のない人は、飛ばしても構いませんが、知っていると便利な場合もあります。
ガンマ線から、電子へのエネルギーの移行は、ガンマ線の進行方向の変化の度合いによるので、
その角度が一番大きいものが、光電ピークの直ぐ左側のコンプトンエッヂで、以下の式で計算出来ます。

http://en.wikipedia.org/wiki/Compton_edge
(meC2)の部分が定数で、511KeVなので、
幾つかのコンピューター言語では、こんな感じ。
Ec = (2 * E ^ 2) / (511 + 2 * E)
Pythonだと
Ec = (2.0 * E ** 2) / (511.0 + 2.0 * E)
Cs137 の場合、大雑把に662KeVとすると、Ec = (2 * 662 ^ 2) / (511 + 2 * 662) = 477.65KeV
バックスキャッターは、元のエネルギーからコンプトンエッジの値を引いて、662 - 477.62 = 184.35KeV
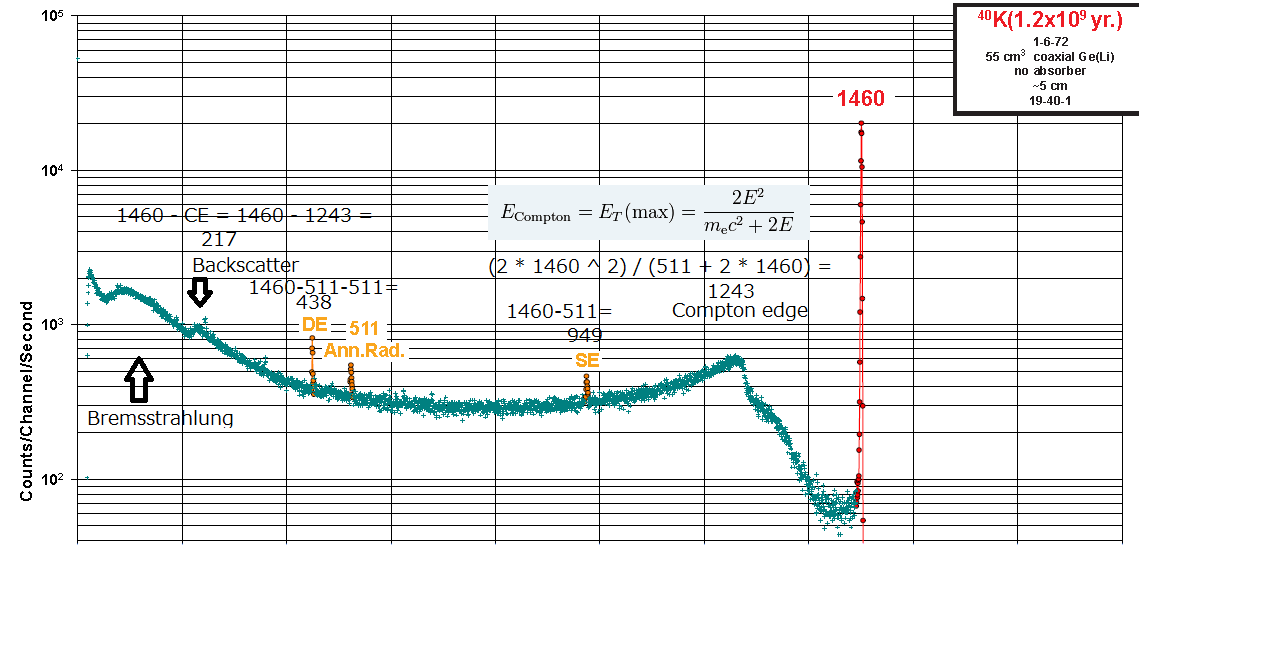
K40 の場合なら、Ec = (2 * 1460 ^ 2) / (511 + 2 * 1460) = 1242.55KeV
バックスキャッターは、 1460 - 1242.55 = 217.45KeV
これらの出方は、クライン仁科の式で計算できるそうで、私もエクセルとかで、両端をゴニョゴニョ計算してみましたが、
エネルギーをガンマ線の波長で捉えている形の計算式が多く、面倒でした。
コンプトン散乱と一緒に良く出てくるシングルエスケープ(SE=Single Escape)とダブルエスケープ(DE)の計算は、
もっと簡単で、光電ピーク(PhotoPeak=pp,PhotoElectricPeak=PEP)のエネルギーから511keVを引くとSE,
511x 2=1022keVを引くとダブルエスケープです。
参考資料
Wikipediaとか
http://ja.wikipedia.org/wiki/%E3%82%B3%E3%83%B3%E3%83%97%E3%83%88%E3%83%B3%E5%8A%B9%E6%9E%9C
こういうのとか、他にも物理の講義の説明などに見つかるでしょう。
http://sapphire.pc.uec.ac.jp/sozai/zenki2010/MPtxt08t.pdf
私は、Am241の線源の向きを変えながら、色々な物に当てて、 その結果出てくる蛍光X線のテキトーな実験をしていて、
Am241の59.5KeVのピークがずれたり、二つに分かれたり、そんな現象を見て、なんじゃこりゃ?とか思って調べたら、
真面目な(物理系の?)学生さんは、フツーに習っている割と基礎的なことだったみたいです。
ちなみに、私がその実験の時にメモしたのが、このページです。(英語です)
http://pico.dreamhosters.com/ComptonScattering.html
虫食い算的に、欠けている数値を計算してくれる便利なページもあります。(英語です)
http://hyperphysics.phy-astr.gsu.edu/Hbase/quantum/compton.html
この講義資料によると、Cs137(662KeV)のコンプトンエッジが441KeV、バックスキャッターピークが181KeV。他で見た計算と違うぞ!特にコンプトンエッジが。
この文書は、途中からCs137のエネルギーを662KeVではなく、622KeVとして計算している為に間違った結果になっています。
http://www.physics.rutgers.edu/ugrad/389/gamma.pdf
これによると、コンプトンエッジのエネルギーは、 Ec = 2 x E x E / (511 + 2 x E)
E=662KeV として計算すると、477KeV。
http://en.wikipedia.org/wiki/Compton_edge
ところが、こっちの資料の6ページ目だと、光電ピークとコンプトンエッジの差のエネルギーは、256KeVになる、みたいなことが書いてある。
まあ、私がテキトーに読んで、勝手に誤解して、混乱している、という可能性もあるんだけど、どうなっているんだろうか?
あ、光電ピークの値が十分に大きい時には、大まかに言って、256KeVくらいだと思ってよい、と言っても、それって、10MeVとか、
普通のガンマ線スペクトル測定よりも相当エネルギーの高い領域の話みたいです。
5ページ目の式だと、コンプトン散乱後のエネルギーE’ = E / (1 + E x ( 1 − CosΘ) / 511)。 角度がゼロに近いと、E’ = Eで、当たり前。
http://socrates.berkeley.edu/~phylabs/adv/ReprintsPDF/COM%20Reprints/01%20-%20Radiation%20Detection%20and%20Measurement%20CH%2010.pdf
こういうのもあります。
http://physics.tamuk.edu/~suson/html/3110/GammaSpectra.htm