Peak Fit With Gnuplot
Gnuplotの使い方にも少し慣れてきたので、テレミノ形式で保存されたガンマスペクトルのピークフィットを試してみることにしました。
注意:私は専門家でも学者でもありませんので、間違っている箇所があるかもしれません。真面目な学生さんなどは、良く検討しないでコピペすると、成績が下がったり落第する可能性があるので気を付けましょう。
参考にしたのは、こちらなどです:
上のサイトが繋がらなかったり、死んでしまった時: http://translate.google.ca/translate?hl=en&sl=ja&tl=en&u=http%3A%2F%2Fwww.stex.phys.tohoku.ac.jp%2Fcomp_text%2Fnode67.html&anno=2
実験データやGnuplotのスクリプト http://web.archive.org/web/20070121224056/http://www.stex.phys.tohoku.ac.jp/jikken/gamma/sample_dir.html
Gnuplotのインストールや使い方は、こちらをご覧下さい。
他に、
Peak Fit With Gnuplot Part2 任意の単一ピーク編、
Peak Fit With Gnuplot Part3 複数ピーク+核種データ編、
Peak Fit With Gnuplot Part4 検出器の特性調査編、
Peak Fit With Gnuplot Part5 検出器の自動特性調査編、
Peak Fit With Gnuplot Part6 色々な関数編があります。
テレミノ形式のスペクトルを表示させる
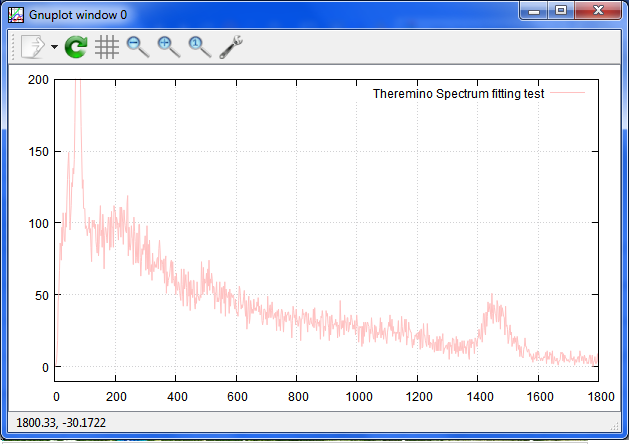
まず、スペクトルを表示させます。
Gnuplotを起動したら、スペクトルが入っているフォルダーをエクスプローラーでコピーするなり、
ファイルの名前をコピーして、簡単に入力出来る様にします。
gnuplot> f="C:\Users\XXX\Theremino_MCA_NaI-3\Data\Test-3-8_TPA_LC4\ThereminoMCA_2015_03_27_15_01_47-Test_3-8_TPA_LC4-N3.txt"
そして、plot コマンドで描画:
gnuplot> plot f using 1:2 every ::50 with line
f に覚えさせた名前のファイルを読み込み、その1番目と2番目の列のデータを使い、最初の50行を無視し、
線で描画する、というものです。
テレミノMCAのバージョンによっては、ヘッダー部分の行数が違うので、ここに正しい数字を入れる必要があります。
(そのうち、この数値も、自動的に発見出来る様にしたいと思っています。)
with line を with dot で点表示、with b で棒グラフ、この部分の指定無しでお任せにも出来ます。
以上のコマンドは、using を短縮して u と書くことも出来ます。
gnuplot> plot f u 1:2 every ::50 with line
グラフが別画面に出たら、適当に画面の大きさを変えて見やすくしてください。
(コマンドで指定することも出来ますが)
横の表示範囲は、 こうとやると、0から2000keVまで表示されます。
gnuplot> set x range [0:2000]
縦は、お任せでも良いでしょう。
gnuplot> set yrange [*:*]
上は、300カウントまで表示する場合。
gnuplot> set yrange [*:300]
または、この様に、 plot に続けて、 横軸、そして縦軸の表示範囲をしてすることも出来ます。
この例では、さらに t (title) でタイトルの指定をして、 lt (linetype) で、色の指定をしています。
gnuplot> plot [0:1800] [-10:200] f u 1:2 every ::50 with line t "Theremino Spectrum fitting test" lt rgb "pink"
とにかくガウス関数でフィットしてみる
で、まずはK40の山にガウス曲線をフィットさせてみます。
ガウス曲線用の関数は、まずは、傾きのある直線をベースラインとして、その上に乗っているものとします。
(そのうち、三次曲線か何かに変える予定。)
これがその式:
gnuplot> g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b
g(x) というのが、関数の名前、h がピークの高さで、スペクトルファイルのデータはカウント数なので、
これもカウント数になります。exp(-((x-E)/s)**2/2) の部分がガウス曲線で、Eがピークのエネルギー(keV)、
s がシグマ(keV)で、釣鐘状の曲線の幅の割合を示します。
a*(x-E)+b がベースラインの直線で、a が傾き、 E がピークのエネルギーで、
b が、ピークの位置におけるベースラインの高さ(カウント数)。
そしたら、まず、これらの変数に「初期値」を入れてやらないとなりません。
h にピークの高さを、おおよそのカウント数で入れます。
E は、K40のエネルギーなので、1460 を入れます。
s は、ピークの幅で、ピークの根元の右側から左のおおよその幅を6で割った値くらいで良いです。
分からない場合は、とりあえず 30 を入れておいてください。
a は、傾きで、-0.001 くらいで試してみてください。
b は、ピークの根元の高さをカウント数で入れてください。分からなかったら、1 とかで良いです。
これを、まとめて書くと、こんな感じ。
gnuplot> h=40;E=1460;s=30;a=-0.001;b=1
初期値の準備が出来たら、早速フィットしてみます。
この時、何シグマまでフィットするのかを n に数字を入れて指定します。
gnuplot> n=3
gnuplot> fit [E-n*s:E+n*s] g(x) f every ::50 noerror using 1:2 via h,E,s,a,b
すると、こんな感じで、数字が沢山出てきます。
iter chisq delta/lim lambda h E s a b 0 9.6304563485e+03 0.00e+00 3.35e+02 4.000000e+01 1.460000e+03 3.000000e+01 -1.000000e-03 1.000000e+00 1 7.0903344100e+03 -3.58e+05 3.35e+01 4.108968e+01 1.457811e+03 3.266800e+01 -1.000020e-03 1.004519e+00 2 2.8262589661e+03 -1.51e+06 3.35e+00 3.705743e+01 1.456779e+03 4.516310e+01 -9.999377e-04 1.080109e+00 3 2.3482544695e+03 -2.04e+05 3.35e-01 3.716618e+01 1.456347e+03 4.899285e+01 -1.015701e-03 1.771745e+00 4 2.3110903607e+03 -1.61e+04 3.35e-02 3.164369e+01 1.456621e+03 4.202431e+01 -4.474592e-03 7.832872e+00 5 2.3033445190e+03 -3.36e+03 3.35e-03 3.187430e+01 1.457464e+03 4.135623e+01 -1.110101e-02 7.809074e+00 6 2.3033199682e+03 -1.07e+01 3.35e-04 3.193025e+01 1.457405e+03 4.148307e+01 -1.081932e-02 7.730278e+00 7 2.3033198246e+03 -6.23e-02 3.35e-05 3.192879e+01 1.457411e+03 4.147751e+01 -1.085521e-02 7.733127e+00 iter chisq delta/lim lambda h E s a b
After 7 iterations the fit converged. final sum of squares of residuals : 2303.32 rel. change during last iteration : -6.23228e-008
degrees of freedom (FIT_NDF) : 79 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 5.39962 variance of residuals (reduced chisquare) = WSSR/ndf : 29.1559
Final set of parameters Asymptotic Standard Error ======================= ========================== h = 31.9288 +/- 3.321 (10.4%) E = 1457.41 +/- 3.117 (0.2138%) s = 41.4775 +/- 5.327 (12.84%) a = -0.0108552 +/- 0.02079 (191.5%) b = 7.73313 +/- 3.637 (47.03%)
correlation matrix of the fit parameters: h E s a b h 1.000 E -0.142 1.000 s 0.813 -0.138 1.000 a 0.200 -0.834 0.183 1.000 b -0.939 0.146 -0.941 -0.205 1.000 gnuplot>
うーん、高さやシグマの標準誤差はともかく、ベースラインの傾きや中央の高さの数字は何なのだ?
コンプトン散乱の丘の上の方から、3次式か何かでベースラインを取るようにしたら、
それをセシウムとかのベースラインにも使えるかもしれないし、不確かさが減るのだろうか?
ともかく、結果をグラフに表示してみようと思いますが
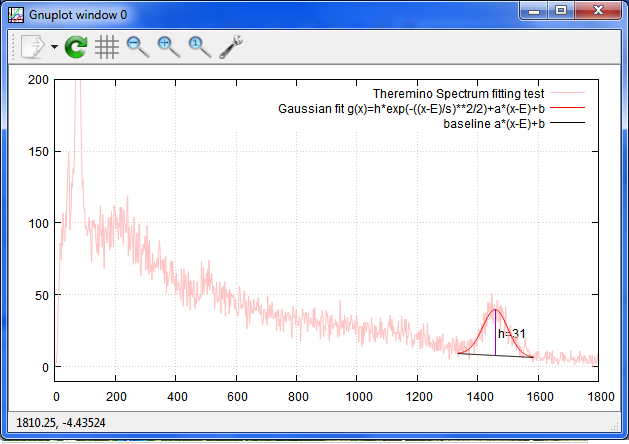
その前に、高さの線を出し、
gnuplot> unset arrow
gnuplot> set arrow from E,b to E,b+h
そのラベルを出します。
gnuplot> unset label
gnuplot> set label sprintf(" h=%d",h) at E,b+h/2 front
そして、スペクトルと、ガウス曲線とベースラインを出します。
gnuplot> plot [0:1800] [-10:200] f u 1:2 every ::50 with line t "Theremino Spectrum fitting test" lt rgb "pink",[E-n*s:E+n*s] g(x) t "Gaussian fit g(x)=h*exp(-((x-E)
/s)**2/2)+a*(x-E)+b" lt rgb "red", [E-n*s:E+n*s] a*(x-E)+b t"baseline a*(x-E)+b" lt rgb "black"
フィットした情報から、ピーク部分の計数率(面積)を出してみる
このガウス関数の全域の面積は、単純に、高さとσ(シグマ)から、こうなります。
面積 = 高さ x √(2π) x σ
これも、Gnuplotに計算してもらいます。
σ(シグマ)は、エネルギーではなく、チャンネル数でないとならないので、
まずテレミノ形式のスペクトルデータのチャンネル配分を2次式の形でフィットして求めます。
この際、上限を指定することが重要です。
この例では、チャンネルの最後が、1886行目で、最初の50行がヘッダーなので、
データは1836行ある筈ですが、丸めて、1800チャンネルでフィットします。
二次式の最初の ca は、エネルギーの高い方で、直線よりも持ち上がるか、下がり気味になるか、
というのを決定し、初期値は適当に 0.0001 くらいを入れておきます。
また、チャンネル勾配が、約2keV/チャンネルなので、cb に 2 を入れ、
下駄はマイナス2だった筈ので、 cc に -2 を入れます。
gnuplot> ecal(x)=ca*x**2+cb*x+cc
gnuplot> ca=0.0001;cb=2;cc=-2
gnuplot> fit [0:1800] ecal(x) f every ::50 noerror using 0:1 via ca,cb,cc
これで、チャンネルからエネルギーは計算できるので、
逆に、エネルギーからチャンネルを求める式も作ります。
gnuplot> e2b(y)=(-cb+sqrt(cb**2-4*ca*(cc-y)))/(2*ca)
ピークのエネルギー位置のチャンネルは、
gnuplot> bE=e2b(E)
それよりもσ(シグマ)の分だけ左のチャンネルは、
gnuplot> bEs1=e2b(E-s)
なので、チャンネル数でのσ(シグマ)は、
gnuplot> bsig=bE-bEs1
なお、このシグマの計算の仕方は、厳密なものではありません。
実用上の問題は無いと思いますが、気になる方は、両側を調べて平均を取るなり、
両側3σの幅で調べて、6で割るなり、お好きにどうぞ。
で、高さと定数とσ(シグマ)をかけると
gnuplot> counts=h*sqrt(2*pi)*bsig
gnuplot> print counts
1548.89527385096
これを測定秒数で割れば、計数率が出て、それに換算係数をかけてやれば総量が出て、それを重量で割れば、濃度になります。
測定秒数は、本来は、Gnuplot で読み出すことは出来ないのですが、
これも、フィットを乱用して、無理矢理読み出します。
関数は、こういうもの。
gnuplot> ff(x)=r*x*sec+sec
初期値は、sec が予想測定秒数で、多分どんな値でも大丈夫でしょう。
gnuplot> sec=3600
r は、おおよその全体の計数率です。測定器や、遮蔽とか、環境によって、適当に入れてください。
なにせ、直線を2点にフィットするだけなので、初期値は何を入れても大丈夫なんじゃないか?という気もします。
gnuplot> r=10
これが、フィット。要は、テレミノ形式のファイルの最初の4行を飛ばして、5行目と6行目を読んでいます。
これで、sec に、測定秒数が入ります。
gnuplot> fit [0:1] ff(x) f noerror u 0:3 every ::4::5 via sec ,r
gnuplot> rate=counts/sec
gnuplot> print rate
0.430368233912463
K40の山が、約0.4cps、というのは、ピーク情報で得られる値と、まあまあ合致しています。
コべル法もどきと比較する
ベースラインが一応分かった(というか、こじつけた)ので、
それでもってBG部分(とみなす面積)が分かり、
その幅の全体の計数(率)が分かれば、
ピーク部分のカウント数や計数率が分かります。
ベースラインの左端のエネルギーは、 E-3*s
右端は、 E+3*s
なので、この情報を使って、Gnuplotの統計機能を使ってみようと思います。
gnuplot> stats [E-3*s:E+3*s] f u 1:2 every ::50::1830
* FILE: Records: 116 Out of range: 1664 Invalid: 0 Blank: 0 Data Blocks: 1
* COLUMNS: Mean: 1458.1828 21.7672 Std Dev: 71.8137 11.5119 Skewness: 0.0027 0.5748 Kurtosis: 1.7999 2.2760 Avg Dev: 61.6897 9.1121 Sum: 169149.2000 2525.0000 Sum Sq.: 2.47249e+008 70335.0000
Mean Err.: 6.6677 1.0689 Std Dev Err.: 4.7148 0.7558 Skewness Err.: 0.2274 0.2274 Kurtosis Err.: 0.4549 0.4549
Minimum: 1335.0000 [ 0] 3.0000 [115] Maximum: 1581.7000 [115] 51.0000 [ 52] Quartile: 1395.9500 13.0000 Median: 1458.1000 19.0000 Quartile: 1520.3500 30.5000
Linear Model: y = -0.01347 x + 41.41 Slope: -0.01347 +- 0.01496 Intercept: 41.41 +- 21.84 Correlation: r = -0.08403 Sum xy: 3.674e+006
色々と出てきましたが、使うのは、Sumのカウント数の方で、2525 です。
これは、STATS_sum_y という内部変数に収められています。
gnuplot> print STATS_sum_y
2525.0
ちなみに、
gnuplot> show all
とやると、内部変数とかが全部見られます。
ここで、生真面目にベースラインの下の面積を、台形を計算して求めても良いのですが、
どうせチャンネル幅と中央の高さをかけたものでしかないので、手抜きします。
チャンネル幅は、
gnuplot> w=e2b(E+3*s)-e2b(E-3*s)
gnuplot> print w
116.042178400715
gnuplot> counts_C=STATS_sum_y-w*b
gnuplot> print counts_C
1627.63104932437
あれ?さっきの値とちょっと違いますねえ。
gnuplot> print counts
1548.89527385096
gnuplot> rate_C=counts_C/sec
gnuplot> print rate_C, rate
0.452245359634447 0.430368233912463
約5%の違いですので、「素人測定」的には、問題ないのですが、
こういう確認をやらないと、とんでもない計算ミスだの勘違いをやらかしていることがありますので。
後は、線量の分かっている検体で、係数を求めたら、それを使えば線量や濃度が分かる、という仕組み。
(ただし、K40に対するCs134の影響とか、ウラン系やトリウム系の影響とか、
そういうものは、まだ全然手を付けてないし、他の補正とかも、全く無しではありますが)
ここまでで出来たこと
要は、ピーク情報機能に於いて、現在は手動でベースラインを決めて、
後は、半自動か手動で曲線を描かせて、数値や山の形を確認する、という
大変手工芸的な方法だったのですが、Gnuplotに初期値を与えてやれば、
後はほぼお任せで、やってくれるわけです。
また、同じことをCs137,Cs134,などなどに対して行ったり、
欲張って、コンプトン散乱のパターンも使っちゃおうじゃないか、とか、
そういうテストをやったり、OctaveやRや他のソフトでやるのと、使い心地や
柔軟性、速度、などなどを比較したり、こういった機能をvbでテレミノMCAに
組み込むのか、外のプログラムを呼び出す形式にするのか、そういうことを
考える材料にしようと思っているわけです。
ヘッダー部分の数字を読み込むマシな?方法
フィットを濫用する代わりに、STATSを悪用します。
この方法の利点は、目当ての行が何行目にあっても、文字列でもって見分けるので超危険派の私でも安全・安心!
#マクロを許可 set macro
#マクロを定義。 #データの区切り文字を、var_sep に変更し、 #statsでもって、var_str の文字列を含む行の数字以外は、ゼロを返す。 #データの区切り文字をリセット。 #var に結果を格納。 var_set='set datafile separator var_sep;\ stats f every ::1::60 u 0:(strstrt(stringcolumn(1),var_str)>0?column(2):0) nooutput;\ unset datafile separator;\ var=STATS_max_y'
#使うときは、最初の1回は区切りを定義。 var_sep=":"
#読み込む行に含まれる文字列を指定 var_str="Total time"
#マクロを呼び出し。この例では、その後に、結果を表示 @var_set;print var
似たような手口で、ヘッダー部分の長さを見つける方法
ファイルの中の任意のパターンを認識することは出来ますし、
それが見つかったときに、任意の値をGnuplotに与えることも出来るので、
色々と悪用が可能です。
#マクロを許可 set macro
#マクロを定義。 #データの区切り文字を、"|" に変更し、 #statsでもって、var_str の文字列を含む行以外は、ゼロを返す。見つかったら、その行番号を返す。 #データの区切り文字をリセット。 #var に結果を格納。 find_line='set datafile separator "|";\ stats f every ::1::60 u 0:(strstrt(stringcolumn(1),var_str)>0?column(0):0) nooutput;\ unset datafile separator;\ var=int(STATS_max_y)'
#調べたい行に含まれる文字列を指定 var_str='Energy(KeV)'
#マクロを呼び出し。 @var_set
#ヘッダー部分の行数 HL=var+2
コマンドをまとめて、もっと自動化
上記の手順を一つか二つのコマンドファイルにまとめて、
もっと自動化します。
で、そしたら、現在手元にある膨大な量のスペクトルでテストしたり、
K40の山が時間と伴にどう上下左右に動くのか?とか、
温度変化や電源電圧の変化でどういう事が起こるのか?とか
そういうことを調べて、それらに対処する可能性を考えたりする材料にします。
まとめて、自動化した実験版コマンドスクリプト
#========================== #Gnuplot でテレミノ形式のスペクトルデータを読んで、 #K40のピークをフィットするコマンドスクリプト
#まず、リセット。これをやらないと、上手くいかないことがある。 reset
#コマンドファイルは、f にファイル名を与えて呼ぶと、 #まず、幾つかの定義をします。
#ヘッダー部分の行数の初期値 HL=50
#マクロを許可 set macro
#四捨五入の関数 round(x,n)=1/(10.0**n)*floor(x*(10**n)+0.5)
#データの区切り文字を、"|" に変更し、 #statsでもって、var_str の文字列を含む行以外は、ゼロを返す。見つかったら、その行番号を返す。 #データの区切り文字をリセット。 #var に結果を格納。 find_line='set datafile separator "|";\ stats f every ::1::var_endline u 0:(strstrt(stringcolumn(1),var_str)>0?column(0):0) nooutput;\ unset datafile separator;\ var=int(STATS_max_y)'
#調べたい行に含まれる文字列を指定 var_str='Energy(KeV)'
#調べるのを止める行を指定 var_endline=100
#マクロを呼び出し。 @find_line
#スキップするヘッダー部分の長さを指定 HL=var+2
#BG(バックグランド)のデータが含まれている場合、その先頭の行数を見つけます。 var_str='BG Data'
#調べるのを止める行を指定 var_endline=100000
#マクロを呼び出し。 @find_line
#BGの先頭をセット BGL=var
#BGがない場合は、テキトーな大きな値にしておく。 if(BGL==0){BGL=var_endline}
#次のマクロを定義。 #データの区切り文字を、var_sep に変更し、 #statsでもって、var_str の文字列を含む行の数字以外は、ゼロを返す。 #データの区切り文字をリセット。 #var に結果を格納。 var_set='set datafile separator var_sep;\ stats f every ::1::60 u 0:(strstrt(stringcolumn(1),var_str)>0?column(2):0) nooutput;\ unset datafile separator;\ var=STATS_max_y'
#使うときは、最初の1回は区切りを定義。 var_sep=":"
#========================== #上で定義したマクロで、測定時間と総カウント数を読み込みます。 var_str="Total time" @var_set;sec=var print "Live Time, sec =", sec
var_str="Pulses per sec" @var_set;r=var print "Total rate, cps =", r
#========================== #テレミノ形式のスペクトルデータのチャンネル配分を2次式の形でフィットして求めます。 #この際、上限を指定することが重要です。
#自動化の為に、まず、200chまでを読み、その値を使って、1500keVのチャンネルを推測し、 #そこまで読みます。
last_ch=200
#二次式の最初の ca は、エネルギーの高い方で、直線よりも持ち上がるか、下がり気味になるか、 #というのを決定し、初期値は適当に 0.0001 くらいを入れておきます。 #また、チャンネル勾配が、約2keV/チャンネルなので、cb に 2 を入れ、 #下駄はマイナス2だった筈ので、 cc に -2 を入れます。
ecal(x)=ca*x**2+cb*x+cc ca=0.0001;cb=2;cc=-2 fit ecal(x) f every ::HL::BGL using 0:1 noerror via ca,cb,cc
#これで、チャンネルからエネルギーは計算できるので、 #逆に、エネルギーからチャンネルを求める式も作ります。
e2b(y)=(-cb+sqrt(cb**2-4*ca*(cc-y)))/(2*ca)
#念のために、1500keVまでに延長し、再フィット。もっとデータがあるのなら、変えると良いでしょう。
#last_ch2=e2b(1500) #fit [0:last_ch2] ecal(x) f every ::HL using 0:1 via ca,cb,cc
#========================== #ピークのフィット #ガウス曲線用の関数は、まずは、傾きのある直線をベースラインとして、その上に乗っているものとします。 g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b
#g(x) というのが、関数の名前、h がピークの高さで、スペクトルファイルはカウント数なので、 #これもカウント数になります。exp(-((x-E)/s)**2/2) の部分がガウス曲線で、Eがピークのエネルギー(keV)、 #s がシグマ(keV)で、釣鐘状の曲線の幅の割合を示します。
#a*(x-E)+b がベースラインの直線で、a が傾き、 E がピークのエネルギーで、 #b が、ピークの位置におけるベースラインの高さ(カウント数)。
#そしたら、まず、これらの変数に「初期値」を入れてやらないとなりません。 #h にピークの高さを、おおよそのカウント数で入れます。 #E は、K40のエネルギーなので、1460 を入れます。 #s は、ピークの幅で、ピークの根元の右側から左のおおよその幅を6で割った値くらいで良いです。 #分からない場合は、とりあえず 30 を入れておいてください。
#a は、傾きで、-0.001 くらいで試してみてください。 #b は、ピークの根元の高さをカウント数で入れてください。分からなかったら、1 とかで良いです。
#これを、まとめて書くと、こんな感じ。この部分は、もっと自動化する予定。 h=40;E=1460;s=30;a=-0.001;b=1
#やっぱり、手動で初期値を入れるのは、間違いやすいし、手間がかかるので #統計機能を使って、ピークの頂点と最低点を適当に推測 # b の初期値は、ゼロだと文句を言われるのでチェックしてゼロなら1を入れる。 stats [1350:1600] f u 1:2 every ::HL::BGL nooutput b=STATS_min_y h=STATS_max_y-b if (b==0){b=1}
#結果の不確かさを変数に保存するよう指定。 set fit errorvariables
#この時、何シグマまでフィットするのかを n に数字を入れて指定します。 #3くらいで良いのではないか、と思ったら、もう少し大きいほうが、もっともらしくなりました。 n=6 fit [E-n*s:E+n*s] g(x) f every ::HL using 1:2 noerror via h,E,s,a,b
#シグマから、FWHMを計算。 σ(シグマ) = FWHM(チャンネル幅) ÷ 2√(2ln2) なので、 fwhm=s * 2*sqrt(2*log(2)) Pfwhm=fwhm/E
peak_h_err=h_err/h*100 peak_s_err=s_err/s*100
#========================== #フィットした情報から、ピーク部分の計数率(面積)を出してみる
#このガウス関数の全域の面積は、単純に、高さとσ(シグマ)から、こうなります。 # 面積 = 高さ x √(2π) x σ
#これも、Gnuplotに計算してもらいます。
#σ(シグマ)は、エネルギーではなく、チャンネル数でないとならないので、 #先ほどデータファイルのエネルギーのカラムを読んでフィットしたチャンネル勾配を使います。
#ピークのエネルギー位置のチャンネルは、 bE=e2b(E)
#それよりもσ(シグマ)の分だけ左のチャンネルは、 bEs1=e2b(E-s)
#なので、チャンネル数でのσ(シグマ)は、 bsig=bE-bEs1 print "sigma(channels) = ", bsig
#なお、このシグマの計算の仕方は、厳密なものではありません。 #実用上の問題は無いと思いますが、気になる方は、両側を調べて平均を取るなり、 #両側3σの幅で調べて、6で割るなり、お好きにどうぞ。
#で、高さと定数とσ(シグマ)をかけると counts=h*sqrt(2*pi)*bsig print "Counts = ", counts
#データファイルから読み出しておいた測定秒で割ってピークの計数率を求めます。 rate=counts/sec print "rate = ", rate
#標準不確かさ U=sqrt(rate/sec)
#========================== #コペル法もどきと比較する
#ベースラインが一応分かった(というか、こじつけた)ので、 #それでもってBG部分(とみなす面積)が分かり、 #その幅の全体の計数(率)が分かれば、 #ピーク部分のカウント数や計数率が分かります。
#ベースラインの左端のエネルギーは、 E-3*s、 右端は、 E+3*s #なので、この情報を使って、Gnuplotの統計機能を使う。 stats [E-3*s:E+3*s] f u 1:2 every ::HL::1830
#色々と出てきましたが、使うのは、Sumのカウント数の方で、 #これは、STATS_sum_y という内部変数に収められています。 #これが、Gross countsに相当します。 counts_G=STATS_sum_y
# レートにすると、 rate_G = STATS_sum_y/sec
#チャンネル幅は、 w=e2b(E+3*s)-e2b(E-3*s)
#BGのカウントとレートは、 counts_BG=w*b rate_BG=counts_BG/sec
#ネットカウントは、 counts_C=STATS_sum_y-counts_BG
#ネットレートは、 rate_C=counts_C/sec
#========================== #結果を表示
print "Time, sec = ", int(sec), " Hr = ", round(sec/3600,2), " day = ", round(sec/3600/24,2)
print "--- Peak fitting ---" print "Peak hight, cts = ", int(h) print "Peak hight rate, cps = ", round(h/sec,5) print "Peak center energy, keV = ", round(E,1) print "Peak center channnel (bin), ch = ", round(bE,2) print "Peak sigma(energy), keV = ", round(s,2) print "Peak sigma(channels), ch = ", round(bsig,2) print "FWHM(energy), keV = ", round(fwhm,2) print "FWHM(channels), ch = ", round(e2b(fwhm),2) print "FWHM, % = ", round(fwhm/E*100,2) print "Peak net Counts = ", int(counts) print "Peak net rate, cps = ", round(rate,5) print "Standard uncertainty (sigma), cps = ", round(U,5), " ", round(U/rate*100,2), " %" print "2 sigma 95%, cps = ", round(2*U,5), round(2*U/rate*100,2), " %" print "3 sigma 99.7%, cps = ", round(3*U,5), round(3*U/rate*100,2), " %" print "Uncertainty from height and width estimate = ",round(sqrt(peak_h_err**2+peak_s_err**2),2), " %" print "--- From stats (and baseline from fit) ---" print "Gross counts, cts = ", int(counts_G) print "Gross rate, = ", round(rate_G,5) print "Net counts, cts = ", int(counts_C) print "Net rate, cps = ", round(rate_C,5) rate_D=rate_C-rate print "DIfference = ", round(rate_D,5), round(rate_D/rate*100,2), " %"
#結果をプロット(このままだと、2番目の拡大の方が見えます。) #書き込み先をファイルにして、両方保存とかすればよいのでしょう。
#全体像 set xrange [0:1800] set yrange [0:*] plot [0:1800] [0:*] f u 1:2 every ::50 with line t "Theremino Spectrum fitting test" lt rgb "pink",[E-n*s:E+n*s] g(x) t "Gaussian fit g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b" lt rgb "red", [E-n*s:E+n*s] a*(x-E)+b t"baseline a*(x-E)+b" lt rgb "black"
#拡大 set xrange [1000:1800] set yrange [0:(h+b)*1.4] Ur=U/rate gh(x,h)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b
plot f u 1:2 every ::50 with line lt rgb "pink" t "Theremino Spectrum" ,\ [E-n*s:E+n*s] g(x) t "Gaussian fit g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b" lt rgb "red",\ [E-n*s:E+n*s] a*(x-E)+b t"baseline a*(x-E)+b" lt rgb "black",\ [E-n*s:E+n*s] gh(x,h*(1+Ur)) lt rgb "light-blue" t "68% 1s", \ [E-n*s:E+n*s] gh(x,h*(1-Ur)) notitle lt rgb "light-blue",\ [E-n*s:E+n*s] gh(x,h*(1+3*Ur)) lt rgb "orange" t "99.7% 3s", \ [E-n*s:E+n*s] gh(x,h*(1-3*Ur)) notitle lt rgb "orange"
実行結果の例:
Time, sec = 13500.0
--- Peak fitting ---
Peak hight, cts = 101.835241680881
Peak hight rate, cps = 0.00754335123562085
Peak center energy, keV = 1457.47129088516
Peak center channnel (bin), ch = 695.907054285008
Peak sigma(energy), keV = 39.5250783399933
Peak sigma(channels), ch = 18.4086138987124
FWHM(energy), keV = 93.0744467564348
FWHM(channels), ch = 46.3906289699306
FWHM, % = 6.38602265022373
Peak net Counts = 4699.03977963694
Peak net rate, cps = 0.348077020713847
Standard uncertainty (sigma), cps = 0.0050777438903356
2 sigma 95%, cps = 0.0101554877806712
3 sigma 99.7%, cps = 0.0152332316710068
Uncertainty from height and width estimate = 1.99454479222119 %
--- From stats (and baseline from fit) ---
Gross counts, cts = 9114.0
Gross rate, = 0.675111111111111
Net counts, cts = 4701.93170484767
Net rate, cps = 0.348291237396123
DIfference = 0.000214216682275892 0.0615428969819867 %
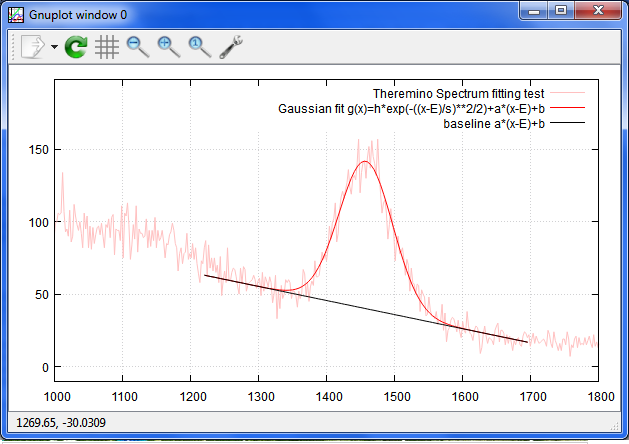
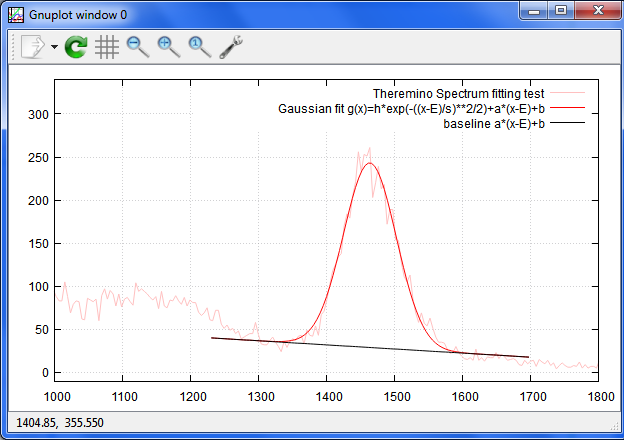
全体像

拡大
粗いチャンネルピッチのファイルで試した例:
粗いチャンネルピッチのファイルで試した例 その2:
スクリプトが強化されています。
(アルマジロ1インチだと1時間くらいに相当)

Time, sec = 178 Hr = 0.05 day = 0.0
--- Peak fitting ---
Peak hight, cts = 6
Peak hight rate, cps = 0.03753
Peak center energy, keV = 1457.8
Peak center channnel (bin), ch = 143.72
Peak sigma(energy), keV = 38.02
Peak sigma(channels), ch = 3.71
FWHM(energy), keV = 89.54
FWHM(channels), ch = 9.97
FWHM, % = 6.14
Peak net Counts = 62
Peak net rate, cps = 0.3488
Standard uncertainty (sigma), cps = 0.04427 12.69 %
2 sigma 95%, cps = 0.08853 25.38 %
3 sigma 99.7%, cps = 0.1328 38.07 %
Uncertainty from height and width estimate = 22.23 %
--- From stats (and baseline from fit) ---
Gross counts, cts = 124
Gross rate, = 0.69663
Net counts, cts = 58
Net rate, cps = 0.32741
DIfference = -0.02139 -6.13 %
粗いチャンネルピッチのファイルで試した例 その3:
上の例のその後の様子です。10倍の時間が経った後。
(アルマジロ1インチだと10時間くらいに相当)

Time, sec = 1799, Hr = 0.5, day = 0.02
--- Peak fitting ---
Peak hight, cts = 69
Peak hight rate, cps = 0.03839
Peak center energy, keV = 1452.6
Peak center channnel (bin), ch = 143.22
Peak sigma(energy), keV = 35.86
Peak sigma(channels), ch = 3.5
FWHM(energy), keV = 84.44
FWHM(channels), ch = 9.47
FWHM, % = 5.81
Peak net Counts = 605
Peak net rate, cps = 0.3365
Standard uncertainty (sigma), cps = 0.01368 4.06 %
2 sigma 95%, cps = 0.02735 8.13 %
3 sigma 99.7%, cps = 0.04103 12.19 %
Uncertainty from height and width estimate = 8.88 %
--- From stats (and baseline from fit) ---
Gross counts, cts = 1184
Gross rate, = 0.65814
Net counts, cts = 615
Net rate, cps = 0.34226
DIfference = 0.00576 1.71 %
細かいチャンネルピッチの短時間のファイルで試した例:
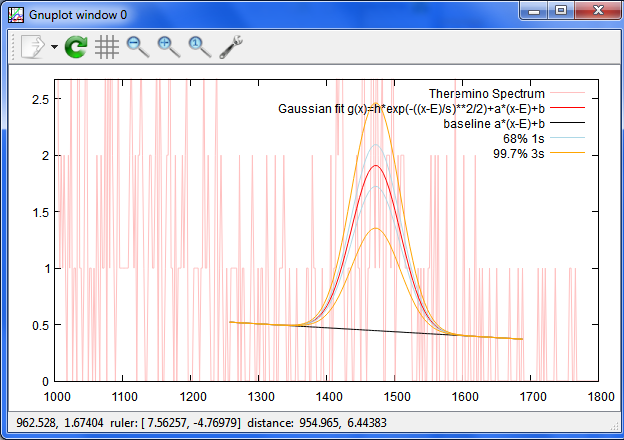
Time, sec = 179, Hr = 0.05, day = 0.0
--- Peak fitting ---
Peak hight, cts = 1
Peak hight rate, cps = 0.00818
Peak center energy, keV = 1472.3
Peak center channnel (bin), ch = 705.46
Peak sigma(energy), keV = 35.79
Peak sigma(channels), ch = 17.05
FWHM(energy), keV = 84.28
FWHM(channels), ch = 42.35
FWHM, % = 5.72
Peak net Counts = 62
Peak net rate, cps = 0.34951
Standard uncertainty (sigma), cps = 0.04419 12.64 %
2 sigma 95%, cps = 0.08838 25.29 %
3 sigma 99.7%, cps = 0.13256 37.93 %
Uncertainty from height and width estimate = 24.4 %
--- From stats (and baseline from fit) ---
Gross counts, cts = 109
Gross rate, = 0.60894
Net counts, cts = 63
Net rate, cps = 0.35413
DIfference = 0.00462 1.32 %
その全体像
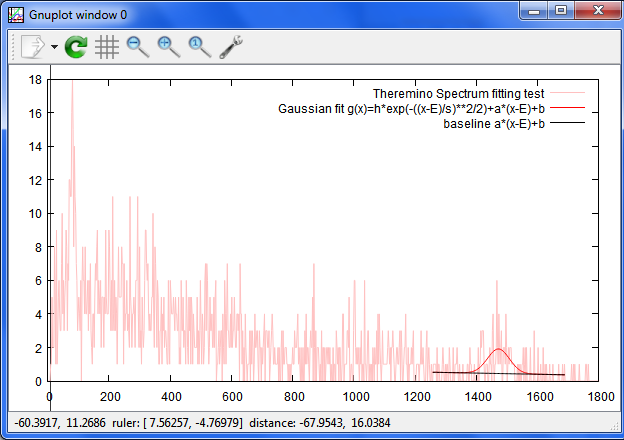
つづく
K40の「単純なフィット」や、あれこれ自動化するのに必要なやり方は分かったので、
Cs137とかCs134といった、セシウムのピークや、K40のコンプトン散乱の取り扱い、とか、
そういう点を試してみるつもりです。
このページは長くなったので、パート2のページを作ります。