Peak Fit With Gnuplot Part2 任意の単一ピーク編
Peak Fit With Gnuplot 最初の一歩とK40編の続編です。
他に、
Peak Fit With Gnuplot Part3 複数ピーク+核種データ編、
Peak Fit With Gnuplot Part4 検出器の特性調査編、
Peak Fit With Gnuplot Part5 検出器の自動特性調査編、
Peak Fit With Gnuplot Part6 色々な関数編があります。
Gnuplotを使ったことの無い方は、まず、 Gnuplot Memo などをご覧になって、
ソフトをインストールする必要があります。
慣れると、3Dスペクトルとかも出来ます。 Fukushima Disaster Spectrum3D Gnuplot Memo3D
K40のフィットが一応少し出来る様になったので、K40のコンプトン散乱の様子とか、
その上に乗るものの様子をやってみようと思います。
で、コンプトン散乱、というか、コンプトンプラトー、コンプトンコンティニュアム、コンプトン丘などの名前で呼ばれる
真ん中が少しへこんだ丘の部分を簡単な方法で推測できると良いのですが、真面目にクライン仁科の式とかで
確認して、そこにバックスキャッターやらX線エスケープやら効率曲線やら分解能を織り込んだりしたものを、
もっと簡単な手抜き曲線でモデル化出来ないか?とか考えてみます。
自分で色々やってみたら、そもそも式が間違っていたりしたので、ちょっと調べたら、
Gnuplot用の式などがありました。
http://wwwpub.zih.tu-dresden.de/~fhgonz/utils/scripts/scripts.php
上記の一部(別バージョン?)
http://wwwpub.zih.tu-dresden.de/~fhgonz/carrera/master/tfm/kn.txt
肝心な部分はこれ。
P(t,E)=1.0/(1.0+E/511.0*(1-cos(t)))
s(t,E)=P(t,E)**3+P(t,E)-P(t,E)**2*sin(t)*sin(t)
これで、0から360度まで普通の座標でプロットして、
その各位置でガウス曲線を書いて、
それの各エネルギーの統計でコンプトン丘が出来るかと思ったら、
なんか上手くいきませんでした。
それに、この方法では、フィットとか出来ないし、
もっと簡単な関数で誤魔化さないと駄目みたいです。
あるいは、数学的に、フィットとかにも使える形の関数で、
良く似たものに出来るのかもしれませんが、
私には歯が立たないので、2次式や直線でやってみることになりそう。
これは、どなたかのマスターか何かの論文で、丁度似たようなことをやっていて、
二次関数でやっているみたいです。
http://medim.sth.kth.se/hl2009/FabianSeitz.pdf
ともかく、まずは、K40,Cs137(662keV),Ann(511keV)、Cs134(いくつか)、Bi214(609keV)くらいを
Statで調べて、そうして、各自下を直線としてFitしてみても良いですし、初期値を割り出し、
K40のコンプトン丘の上のものを放物線をベースラインにしてFitしてみて、どれくらい合うのか
合わないのか、試してみようと思います。
で、前回K40のフィット使ったスクリプトから、最初に一回だけやっておけばよい部分をまとめて、
一つのスクリプトにします。
使い方は、簡単。fにファイルの名前を入れて、スクリプトをロードするだけで、準備完了。
f='ThererminoMCA-2015-04-01_test.txt'
load 'ft0.plt'
http://pico.dreamhosters.com/raddata/ft0.plt
#========================== #Gnuplot でテレミノ形式のスペクトルデータを読んで、 #色々なピークのフィットする為の準備用コマンドスクリプト
#コマンドファイルは、f にファイル名を与えて呼ぶと、 #まず、幾つかの定義をします。
#リセット reset
#マクロを許可 set macro
#スクリプトの実行が簡単に出来る様に、マクロ用の文字列を登録。 #こうすると、Gnuplotのコマンドラインで、@ft0 とやると、このスクリプトが実行されます。 ft0='load "ft0.plt"' ft1='load "ft1.plt"' nl1='load "nl.plt"' nl2='load "nl2.plt"' nl3='load "nl3.plt"'
# 見つけた(複数の)ピークをプロットする時のオプション。0は表示無し。1は、ベースライン上。2は、グラフの下。3は、両方 popt=1
# エネルギー校正もフィットするかどうか。Energy calibration fit efit=0
# シグマ(FWHMと連動)のフィットをするかどうか Sigma (FWHM) fit sfit=0
# スペクトルの表示用マクロ。line type lt='dot' pinkline='line lt rgb "pink"' lt=pinkline
#四捨五入の関数 round(x,n)=1/(10.0**n)*floor(x*(10**n)+0.5)
#ヘッダー部分の行数の初期値 HL=50
#テレミノ形式のデータの中から、ヘッダーの部分を飛ばしたり、(新方式で追加された)BGスペクトルのデータの前で #読むのを終了するために、それらの行番号を自動的に調べます。
#===特定の文字列がある行を発見するためのマクロ=== # #データの区切り文字を、"|" に変更し、 #statsでもって、var_str の文字列を含む行以外は、ゼロを返す。見つかったら、その行番号を返す。 #データの区切り文字をリセット。 #var に結果を格納。
find_line='set datafile separator "|";\ stats f every ::1::var_endline u 0:(strstrt(stringcolumn(1),var_str)>0?column(0):0) nooutput;\ unset datafile separator;\ var=int(STATS_max_y)'
#上のマクロで、データが始まる直前にある文字列を検索します。
#調べたい行に含まれる文字列を指定 var_str='Energy(KeV)'
#調べるのを止める行を指定 var_endline=100
#マクロを呼び出し。 @find_line
#スキップするヘッダー部分の長さを指定 HL=var+2
#同じマクロを使って、BG(バックグランド)のデータが含まれている場合、その先頭の行数を見つけます。 var_str='BG Data'
#調べるのを止める行を指定 var_endline=100000
#マクロを呼び出し。 @find_line
#BGの先頭をセット BGL=var
#BGがない場合は、テキトーな大きな値にしておく。 if(BGL==0){BGL=var_endline}
#===データファイルの設定を読み込むマクロを定義。===
#データの区切り文字を、var_sep に変更し、 #statsでもって、var_str の文字列を含む行の数字以外は、ゼロを返す。 #データの区切り文字をリセット。 #var に結果を格納。
var_set='set datafile separator var_sep;\ stats f every ::1::60 u 0:(strstrt(stringcolumn(1),var_str)>0?column(2):0) nooutput;\ unset datafile separator;\ var=STATS_max_y'
#使うときは、最初の1回は区切りを定義。 var_sep=":"
#========================== #上で定義したマクロで、測定時間と総カウント数を読み込みます。 var_str="Total time" @var_set;sec=var print "Live Time, sec =", sec
var_str="Pulses per sec" @var_set;r=var print "Total rate, cps =", r
#========================== #テレミノ形式のスペクトルデータのチャンネル配分を2次式の形でフィットして求めます。 #この際、上限を指定することが重要ですが、既に自動的に検索して、BGLという変数に入っています。
#二次式の最初の ca は、エネルギーの高い方で、直線よりも持ち上がるか、下がり気味になるか、 #というのを決定し、初期値は適当に 0.0001 くらいを入れておきます。 #また、チャンネル勾配が、約2keV/チャンネルなので、cb に 2 を入れ、 #下駄はマイナス2だった筈ので、 cc に -2 を入れます。
ecal(x)=ca*x**2+cb*x+cc ca=0.0001;cb=2;cc=-2 fit ecal(x) f every ::HL::BGL using 0:1 noerror via ca,cb,cc
#フィットして求めた値を念のため保存。(後で、ピークフィットの時の結果と比較したりするため) ca0=ca;cb0=cb;cc0=cc
#これで、チャンネルからエネルギーは計算できるので、 #逆に、エネルギーからチャンネルを求める式も作ります。
e2b(y)=(-cb+sqrt(cb**2-4*ca*(cc-y)))/(2*ca)
#初期の校正用を使ったエネルギー=>チャンネル変換の関数 e2b0(y)=(-cb0+sqrt(cb0**2-4*ca0*(cc0-y)))/(2*ca0)
#初期の校正によるエネルギーから、ピークフィットなどの結果から得た現在の校正によるエネルギーに変換する関数。 ee(x)=b2e(e2b0(x))
#========================== #ピークのフィットの準備 #ガウス曲線用の関数は、まずは、傾きのある直線をベースラインとして、その上に乗っているものとします。 g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b
#任意の位置に任意のガウス曲線を出すための関数 gg(x,h,E,s,a,b)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b
#エネルギーから分解能を求める式を追加。
#標準的な 3インチ NaI FWHM 22keV at 122 keV, 50keV at 662keV FWHM122=22 FWHM662=50
#一時式のパラメーターを計算。 fwhma=(FWHM662-FWHM122)/(662.0-122) fwhmb=FWHM662-fwhma*662
#シグマとFWHM(keV)の変換用の定数 s2fwhm = 1/(2*sqrt(2*log(2)))
#任意のエネルギーのシグマを求める関数 SigE(E) = (fwhma * E + fwhmb)* s2fwhm
#文字列操作用の関数も入れておきます。
#文字列 s を最初の sep で分けた頭 cut_after(s,sep) = s[:strstrt(s,sep)-1] #文字列 s を最初の sep で分けた尻尾 cut_before(s,sep) = s[strstrt(s,sep)+strlen(sep):] #文字列 h の最後の最後の n の位置を見つける補助用の再帰関数。 strrstrts(h,n) = (strstrt(h,n) >= 1? strrstrts(h[2:],n): strlen(h)) #文字列 h の最後の最後の n の位置を見つける関数。 strrstrt(h,n) = strlen(h)-strrstrts(h,n) #文字列 s を最後の sep で分けた頭 cut_after_last(h,n) = h[:strrstrt(h,n)-1] #文字列 s を最後の sep で分けた尻尾 cut_before_last(h,n) = h[strrstrt(h,n)+strlen(n):]
#fにフルパスが入っている場合、ファイル名だけを抜き出します。 fn=cut_before_last(f,'\')
#プロットする時のタイトル用のマクロ。ファイル名+測定秒数 ftitle=sprintf("t '%s %d sec'",fn,sec)
#タイトルが、下線などで下付き文字にならないように指定 set termoption noenhanced
#スペクトルを表示して、準備終了 set yrange [0:*] plot [0:2800] f every ::HL::BGL u 1:($2/sec) @lt @ftitle
次が、ピークについての部分で、ここは、Eにピークのエネルギーを与えて
スクリプトを呼び出すだけ。
すると、ピークについての情報を書き出して、拡大図をプロットします。
(全体像を見たいときは、
E=662
n=3
load 'ft1.plt'
http://pico.dreamhosters.com/raddata/ft1.plt
#====================== #任意のエネルギーの単一ピークを指定したシグマの幅でフィット #あらかじめ、ft0.plt を実行して準備がなされている必要があります。
#Statsコマンドなどで問題が起きない様、レンジ設定を解除 unset xrange unset yrange
#Statsコマンドなどで問題が起きない様、Log表示設定を解除 unset logscale
#指定されたエネルギーを変数に保存。 #これは、フィットの時にEの値も変化する為。 Eini = E
#指定されたエネルギー位置のシグマ(分解能)を計算。 s=SigE(E)
#ベースラインの傾きの初期値を適当に設定。 a=-0.001
#統計機能を使って、ピークの頂点と最低点を適当に推測。カウント数で入っているデータを秒数で割って、レートで計算。 print round(E-3*s,2),round(E+3*s,2) stats [E-3*s:E+3*s] f u 1:($2/sec) every ::HL::BGL nooutput b=STATS_min_y h=STATS_max_y-b if (b==0){b=1}
#結果の不確かさを変数に保存するよう指定。 set fit errorvariables
#この時、何シグマまでフィットするのかを n に数字を入れて指定しますが #n が定義されていなかったり、0だった場合は、暫定的に3にしてみる。 if((!exists("n")) || n==0){ n=3}
#フィットの際にも、データ(カウント数)を測定秒数で割って、レートでやります。ピークの高さだけでなく、 #エネルギー位置、分解能、ベースラインの傾きと高さも、全部フィットします。 fit [E-n*s:E+n*s] g(x) f every ::HL using 1:($2/sec) noerror via h,E,s,a,b
#過去の実験の残骸・・・ #nn=2 #fit [E-n*s:E+n*s] ((E-nn*s<x && x<E+nn*s)?g(x):0) f every ::HL using 1:((E-nn*s<x && x<E+nn*s)?$2:0) noerror via h,E,s,a,b #fit [E-n*s:E+n*s] ((E-nn*s<x && x<E+nn*s)?g(x):0) f every ::HL using 1:2 noerror via h,E,s,a,b
#シグマから、FWHMを計算。 σ(シグマ) = FWHM(チャンネル幅) ÷ 2√(2ln2) なので、 fwhm=s * 2*sqrt(2*log(2)) Pfwhm=fwhm/E
peak_h_err=h_err/h*100 peak_s_err=s_err/s*100
#========================== #フィットした情報から、ピーク部分の計数率(面積)を出してみる
#このガウス関数の全域の面積は、単純に、高さとσ(シグマ)から、こうなります。 # 面積 = 高さ x √(2π) x σ
#これも、Gnuplotに計算してもらいます。
#σ(シグマ)は、エネルギーではなく、チャンネル数でないとならないので、 #先ほどデータファイルのエネルギーのカラムを読んでフィットしたチャンネル勾配を使います。
#ピークのエネルギー位置のチャンネルは、 bE=e2b(E)
#それよりもσ(シグマ)の分だけ左のチャンネルは、 bEs1=e2b(E-s)
#なので、チャンネル数でのσ(シグマ)は、 bsig=bE-bEs1 print "sigma(channels) = ", bsig
#なお、このシグマの計算の仕方は、厳密なものではありません。 #実用上の問題は無いと思いますが、気になる方は、両側を調べて平均を取るなり、 #両側3σの幅で調べて、6で割るなり、お好きにどうぞ。
#で、高さと定数とσ(シグマ)をかけると counts=h*sqrt(2*pi)*bsig*sec print "Counts = ", counts
#データファイルから読み出しておいた測定秒で割ってピークの計数率を求めます。 rate=counts/sec print "rate = ", rate
#標準不確かさ U=sqrt(rate/sec)
#========================== #コペル法もどきと比較する
#ベースラインが一応分かった(というか、こじつけた)ので、 #それでもってBG部分(とみなす面積)が分かり、 #その幅の全体の計数(率)が分かれば、 #ピーク部分のカウント数や計数率が分かります。
#ベースラインの左端のエネルギーは、 E-3*s、 右端は、 E+3*s #なので、この情報を使って、Gnuplotの統計機能を使う。 stats [E-3*s:E+3*s] f u 1:2 every ::HL::1830 nooutput
#色々と出てきましたが、使うのは、Sumのカウント数の方で、 #これは、STATS_sum_y という内部変数に収められています。 #これが、Gross countsに相当します。 counts_G=STATS_sum_y
# レートにすると、 rate_G = STATS_sum_y/sec
#チャンネル幅は、 w=e2b(E+3*s)-e2b(E-3*s)
#BGのカウントとレートは、 counts_BG=w*b rate_BG=counts_BG/sec
#ネットカウントは、 counts_C=STATS_sum_y-counts_BG
#ネットレートは、 rate_C=counts_C/sec
#========================== #結果を表示
print fn print "Time, sec = ", int(sec), ", Hr = ", round(sec/3600,2), ", day = ", round(sec/3600/24,2)
print "--- Peak fitting --- n=",n print "Peak hight, cts = ", int(h*sec) print "Peak hight rate, cps = ", round(h,5) print "Peak center energy, keV = ", round(E,1) print "Peak center channnel (bin), ch = ", round(bE,2) print "Peak sigma(energy), keV = ", round(s,2) print "Peak sigma(channels), ch = ", round(bsig,2) print "FWHM(energy), keV = ", round(fwhm,2) print "FWHM(channels), ch = ", round(e2b(fwhm),2) print "FWHM, % = ", round(fwhm/E*100,2) print "Peak net Counts = ", int(counts) print "Peak net rate, cps = ", round(rate,5) print "Standard uncertainty (sigma), cps = ", round(U,5), " ", round(U/rate*100,2), " %" print "2 sigma 95%, cps = ", round(2*U,5), round(2*U/rate*100,2), " %" print "3 sigma 99.7%, cps = ", round(3*U,5), round(3*U/rate*100,2), " %" print "Uncertainty from height and width estimate = ",round(sqrt(peak_h_err**2+peak_s_err**2),2), " %" print "--- From stats (and baseline from fit) ---" print "Gross counts, cts = ", int(counts_G) print "Gross rate, = ", round(rate_G,5) print "Net counts, cts = ", int(counts_C) print "Net rate, cps = ", round(rate_C,5) rate_D=rate_C-rate print "DIfference = ", round(rate_D,5)," ", round(rate_D/rate*100,2), " %"
arr=sprintf("%f, ", Eini, E, h, s, a, b, fwhm, bE, sec, counts, rate, U, counts_G, rate_G, counts_C, rate_C)
#プロットする時のタイトル用のマクロ。ファイル名+測定秒数+n ftitle=sprintf("t '%s %d sec, n=%0.2f'",fn,sec,n)
#全体像 set xrange [0:1800] set yrange [0:*] #plot [0:1800] [0:*] f u 1:2 every ::50 with @lt @ftitle,[E-n*s:E+n*s] g(x) t "Gaussian fit g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b" lt rgb "red", [E-n*s:E+n*s] a*(x-E)+b t"baseline a*(x-E)+b" lt rgb "black" pla='set xrange [0:1800];plot [0:1800] f u 1:($2/sec) every ::50 with '.lt.' '.ftitle.',[E-n*s:E+n*s] g(x) t "Gaussian fit g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b" lt rgb "red", [E-n*s:E+n*s] a*(x-E)+b t"baseline a*(x-E)+b" lt rgb "black" '
#拡大 set xrange [E-(n+3)*s:E+(n+3)*s] set yrange [-0.1:(h+b)*1.4] Ur=U/rate gh(x,h)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b
plot f u 1:($2/sec) every ::50 with @lt @ftitle ,\ [E-n*s:E+n*s] g(x) t "Gaussian fit g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b" lt rgb "red",\ [E-n*s:E+n*s] a*(x-E)+b t"baseline a*(x-E)+b" lt rgb "black",\ [E-n*s:E+n*s] f u 1:((E-n*s<$1 && $1<E+n*s)?$2/sec-g($1):1/0) t "Residuel" with line lt rgb "light-green",\ [E-n*s:E+n*s] gh(x,h*(1+Ur)) lt rgb "light-blue" t "68% 1s",\ [E-n*s:E+n*s] gh(x,h*(1-Ur)) lt rgb "light-blue" notitle,\ [E-n*s:E+n*s] gh(x,h*(1+3*Ur)) lt rgb "orange" t "99.7% 3s",\ [E-n*s:E+n*s] gh(x,h*(1-3*Ur)) lt rgb "orange" notitle
q
以前にメープルシロップを灰化して、CsI2.5インチで測定したファイルを指定してE=662で
ピークを調べた結果の画像

全体像(Logscaleで出してあります。)
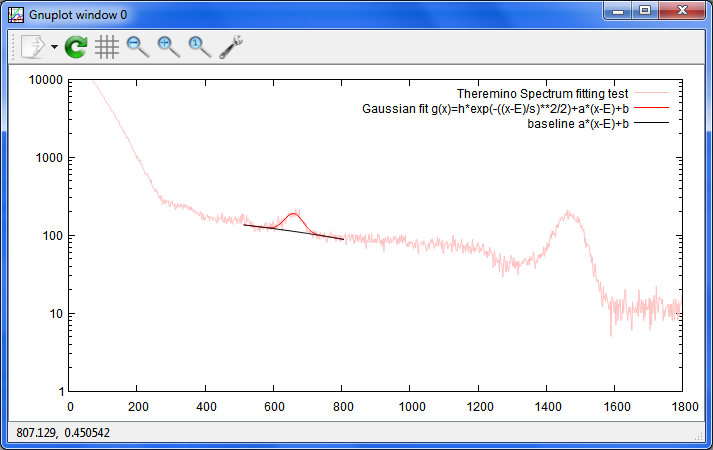
これで、任意の単一ピークの情報が簡単に得られる様になりました。
スクリプトは、改造して、カウント数ではなく、レートで計算、表示するようにして、
フィットとの差分も出す様にしたり、多少変更しました。
次は、複数ピークのフィットやプロットです。
まず、Cs137とCs134の合体ピークで実験

つづきの複数ピークや核種データ対応編は、別のページに作ります