Peak Fit With Gnuplot Part5 検出器の自動特性調査編
Peak Fit With Gnuplot 最初の一歩とK40編、
Peak Fit With Gnuplot Part2 任意の単一ピーク編、
Peak Fit With Gnuplot Part3 複数ピーク+核種データ編、
Peak Fit With Gnuplot Part4 検出器の特性調査編の続編です。
他に、
Peak Fit With Gnuplot Part6 色々な関数編があります。
Gnuplotの色々な使い方は、以下のページに書いてあります。
Gnuplot Memo
Gnuplot Memo3D
Gnuplot Memo2
今回は、特性調査に使うデータを自動で取得し、その結果も自動的にプロットしよう、というものです。
まず、 Peak Fit With Gnuplot Part2 任意の単一ピーク編で作った準備用スクリプトをそのまま使います。
次に、単一ピーク用のスクリプトを改造して、連続して複数のピークに対して調査やフィットを行い、
そのデータをGnuplotが読み込める形でファイルに書き出すようにします。
この時、 Peak Fit With Gnuplot Part3 複数ピーク+核種データ編のころから作り始めた、核種データスクリプトを利用します。
で、単一ピーク用のスクリプトに何をしたか?といいますと、核種のリストでループするようにしたのと、
ピークをフィットする際に、どの範囲でフィットするか?というのが大事なので、それをStatsコマンドで事前調査して、
隣と被っているピークは、狭い幅でフィットし、被ってなかったら広めでフィットする、という作戦です。
尚、このスクリプトは、データの取得部分と、結果の調査、プロット部分に分かれています。
また、サイトにアップロードしてあるスクリプトは、時々改造、改良、改悪して変更されています。
まず、データ取得と書き出し部分。
#====================== #検出器の特性を自動的に調査するためのスクリプト #あらかじめ、ft0.plt を実行して準備がなされている必要があります。 #Automatic peak info checker and detector profile maker
#ft0.plt が実行されてなかったりして、ファイル名とかが定義してない場合は、ft0.pltをまず呼ぶ。 if(!exists("f") || !exists("fname") ||fname ne f){ load 'ft0.plt' }
#しつこくマクロの使用を宣言して、このスクリプトも @ft3 というコマンドで実行できるようにする。 set macro ft3='load "ft3.plt"'
#Statsコマンドなどで問題が起きない様、レンジ設定を解除 unset xrange unset yrange
#Statsコマンドなどで問題が起きない様、Log表示設定を解除 unset logscale
#何シグマまでフィットするのかを n に数字を入れて指定しますが #n が定義されていなかったり、0だった場合は、暫定的に3にしてみる。 if((!exists("n")) || n==0){ n=3}
#この変数が重要で、ピークの左右の最低地点の何倍までの範囲をフィットするかの変数 #これを変えて、色々試せます。ユーザーが定義しない場合は、0.9になります。 if((!exists("sfac")) || sfac==0){ sfac=0.9}
#核種データを読み込みます。 load 'nlist.plt'
#調査に使う核種と、そのピークを指定します。これを変えると、他の核種でやったり、 #特定のピークを入れたり、省いたり出来ます。 #また、核種データと同じ形式で、架空の名前でリストを作り、それを指定しても良いです。 peak_list='Ra226 5 2 3 4 1 7 10 11 17 21'
#ベースラインの傾きの初期値を適当に設定。 a=-0.001
#フィットの結果を変数に指定するおまじない set fit errorvariables
#調査に使用する核種の名前を変数に読み込み。 ri=word(peak_list,1)
#調査結果を書き込むファイルの名前を定義。 pfn=ri.'-dr.plt'
#ファイルを上書きモードで開き、ヘッダー部分を書き込んでリセット。 set print pfn print '# E (keV) Ig (%) ch FWHM (%) h (cps) Np (cps) a b ns0 ns1'
#調査するピークの数+1を変数にセット。 wn=words(peak_list)
#ピークの数だけループ(2から始めるので) do for[i=2:wn] { #ピーク番号をリストから抽出 nn=word(peak_list,i)
#ピーク名の変数を定義 cmd='peakname="'.ri.'_'.nn.'"' eval cmd
#そのピークのエネルギーをEに入れる。 cmd='E=word('.peakname.',1)' eval cmd
#E0にエネルギーを保存。 E0=E
#放出率をIgに設定。 cmd='Ig=word('.peakname.',2)' eval cmd
#指定されたエネルギー位置のシグマ(分解能)を計算。 s=SigE(E) s0=s
#統計機能を使って、ピークの頂点と最低点を適当に推測。カウント数で入っているデータを秒数で割って、レートで計算。 #print round(E-3*s,2),round(E+3*s,2) stats [E-3*s:E+3*s] f u 1:($2/sec) every ::HL::BGL nooutput b=STATS_min_y h=STATS_max_y-b
#bの初期値がゼロだとこけるので、その場合は、1にしておく。 if (b==0){b=1}
#統計調査の結果から、このピークの部分のおおよその傾きと平均の高さや最低の位置などを取得。 sta=STATS_slope stb=STATS_intercept a=stb stm=STATS_mean_y stmin=STATS_min_y
#ピークの傾きを打ち消す関数 bt(x)=sta*x+stb-(stm-stmin) #plot [E-3*s:E+3*s] f every ::HL::BGL u 1:($2/sec), f every ::HL::BGL u 1:($2/sec-bt($1)+stmin),bt(x),stmin
#傾きをある程度打ち消した状態で、ピークの左側の最低地点を調べる stats [E-3*s:E] f u 1:($2/sec-bt($1)+stmin) every ::HL::BGL nooutput min0x=STATS_pos_min_y min0y=STATS_min_y
#傾きをある程度打ち消した状態で、ピークの右側の最低地点を調べる #check right side for the lowest point stats [E:E+3*s] f u 1:($2/sec-bt($1)+stmin) every ::HL::BGL nooutput min1x=STATS_pos_min_y min1y=STATS_min_y
min(x)=((min1y-min0y)/(min1x-min0x))*(x-min1x)+min1y #plot [E-3*s:E+3*s] f every ::HL::BGL u 1:($2/sec), f every ::HL::BGL u 1:($2/sec-bt($1)+stmin),bt(x),stmin,min(x) #ピークの位置から左右の最低地点までの距離をシグマで割り、係数をかけてフィットする範囲を決定。 ns0=(E-min0x)/s*sfac ns1=(min1x-E)/s*sfac
#フィットの際にも、データ(カウント数)を測定秒数で割って、レートでやります。ピークの高さだけでなく、 #エネルギー位置、分解能、ベースラインの傾きと高さも、全部フィットします。 fit [E-ns0*s:E+ns1*s] g(x) f every ::HL using 1:($2/sec) noerror via h,E,s,a,b
#シグマから、FWHMを計算。 σ(シグマ) = FWHM(チャンネル幅) ÷ 2√(2ln2) なので、 fwhm=s * 2*sqrt(2*log(2)) Pfwhm=fwhm/E
peak_h_err=h_err/h*100 peak_s_err=s_err/s*100
#========================== #フィットした情報から、ピーク部分の計数率(面積)を出してみる #このガウス関数の全域の面積は、単純に、高さとσ(シグマ)から、こうなります。 # 面積 = 高さ x √(2π) x σ #これも、Gnuplotに計算してもらいます。
#σ(シグマ)は、エネルギーではなく、チャンネル数でないとならないので、 #ft0 データファイルのエネルギーのカラムを読んでフィットしたチャンネル勾配を使います。
#ピークのエネルギー位置のチャンネルは、 bE=e2b(E)
#それよりもσ(シグマ)の分だけ左のチャンネルは、 bEs1=e2b(E-s)
#なので、チャンネル数でのσ(シグマ)は、 bsig=bE-bEs1 # print "sigma(channels) = ", bsig
#なお、このシグマの計算の仕方は、厳密なものではありません。 #実用上の問題は無いと思いますが、気になる方は、両側を調べて平均を取るなり、 #両側3σの幅で調べて、6で割るなり、お好きにどうぞ。
#で、高さと定数とσ(シグマ)をかけると rate=h*sqrt(2*pi)*bsig # print "rate = ", rate
#データファイルから読み出しておいた測定秒でピークの計数を求めます。 counts=rate*sec # print "Counts = ", counts
#標準不確かさ U=sqrt(rate/sec) #ファイルを閉じて、画面に情報を書き出します。 unset print print sprintf('%f %f %f %f %f %f %f %f %f %f %f',E0+0,Ig+0,bE,fwhm,Pfwhm,h,rate,a,b,ns0,ns1)
#追加書き込みモードでファイルを開き、データを書き込みます。 set print pfn append print sprintf('%f %f %f %f %f %f %f %f %f %f %f',E0+0,Ig+0,bE,fwhm,Pfwhm,h,rate,a,b,ns0,ns1)
#使われていないプロットの残骸。 if(0){ set xr [E-8*s:E+8*s] plot f u 1:($2/sec) every ::50 with @lt @ftitle ,\ [E-ns0*s:E+ns1*s] g(x) t "Gaussian fit g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b" lt rgb "red",\ [E-6*s:E-ns0*s] g(x) t "Gaussian fit g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b" lt rgb "blue",\ [E+ns1*s:E+6*s] g(x) t "Gaussian fit g(x)=h*exp(-((x-E)/s)**2/2)+a*(x-E)+b" lt rgb "blue",\ [E-6*s:E+6*s] a*(x-E)+b t"baseline a*(x-E)+b" lt rgb "black" } }
#全部調査が終わったら、ファイルを閉じます。 unset print
#次の操作の為のマクロを定義して、呼び出します。 ft4='load "ft4.plt"' @ft4
次に、書き出したピークデータを読み込んで、フィットしたり、プロットする部分。
これは、もっと色々追加しても良いし、いちいち画面にプロットせずに、
PNGファイルとかを作っても良いし、校正情報や効率曲線のデータだけとっても良いし、
各自好きなようにしてください。
この例では、エネルギー校正用のフィットとプロットを、直線と二次式でやってみて、
効率曲線のフィットを、ピークの高さと、ピークの面積についてやってみてます。
一つのフィットとプロットの後、ポーズが入っていて、キーボードやマウスで
次のフィットとプロットに進みます。
ここは、基本的に、Part4でやっていたのと同じことで、それをまとめて、
ポーズを入れて、グラフの出し方とかを少し改良したものです。
http://pico.dreamhosters.com/raddata/ft4.plt
#フィットに使う一次関数と二次関数を定義 f1(x)=a*x+b f2(x)=a*x**2+b*x+c
#初期値を適当にセット a=0.5 b=1 c=1
#まずは、エネルギーとチャンネル番号をフィット fit f1(x) pfn u 1:3 via a,b
#プロットにグリッドを出したり、見出しを付けて、表示。 set grid set ylabel 'channel' unset yr
#フィットの結果の数値を数式に混ぜて表示。 fitt=sprintf('f1(x) = %f * x + %f',a,b)
#フィット範囲のファクターも差分のところに表示。 difft=sprintf('diff (sfac=%0.2f)',sfac)
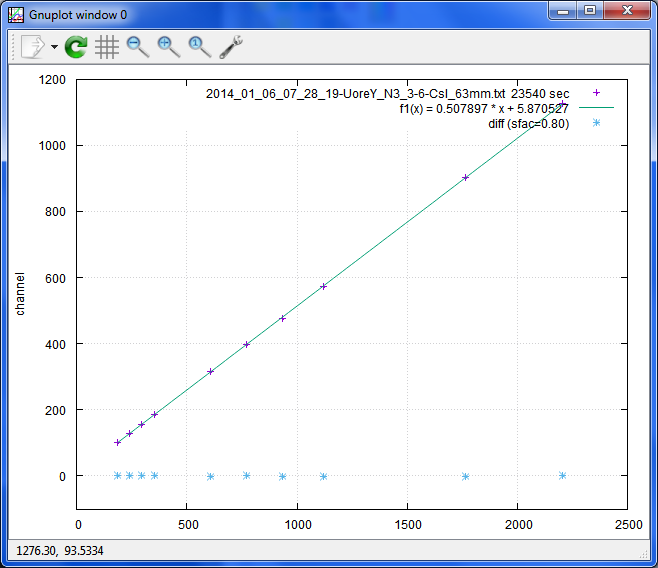
#プロットしてポーズ。 plot pfn u 1:3 @ftitle ,f1(x) t fitt,pfn u 1:($3-f1($1)) t difft pause -1
#次は、エネルギー校正を二次式でフィット。これは、多分、平方根でやるのが正しいのかも。 a=-0.00001 b=0.5 c=1
fit f2(x) pfn u 1:3 via a,b,c
fitt=sprintf('f(x) = %f * x**2 + %f * x + %f',a,b,c) plot pfn u 1:3 @ftitle ,f2(x) t fitt,pfn u 1:($3-f2($1)) t difft pause -1
#次は、効率曲線で、ピークの高さでもってやっています。面積でやるより、この方がまとまる場合が多い。 set ylabel 'Peak hight/sec/Ig'
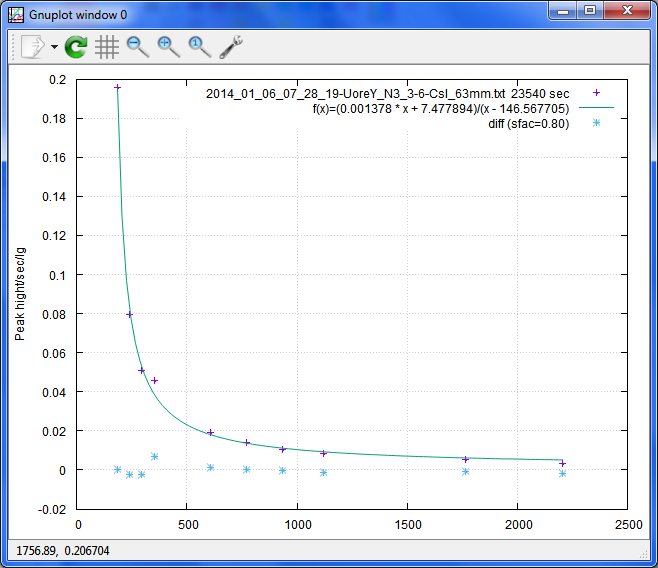
f(x)=(a*x+b)/(x-c) a=0.0001 b=50 c=50 fit f(x) pfn u 1:($6/$2) via a,b,c fitt=sprintf('f(x)=(%f * x + %f)/(x - %f)',a,b,c) plot pfn u 1:($6/$2) @ftitle, f(x) t fitt, pfn u 1:($6/$2-f($1)) t difft pause -1
#今度は、ピークの面積で、効率曲線のフィットをしてますが、その結果を高さに変換したりはまだしていません。 set ylabel 'Peak Rate/sec/Ig'
a=1 fit f(x) pfn u 1:($7/$2) via a,b,c fitt=sprintf('f(x)=(%f * x + %f)/(x - %f)',a,b,c) plot pfn u 1:($7/$2) @ftitle, f(x) t fitt, pfn u 1:($7/$2-f($1)) t difft
#後は、何でも好きな項目を追加したり、変更すればよいでしょう。
sfacの値を大きくしすぎると、フィットに失敗して、良いデータが取れない場合がありますし、
小さすぎても同じです。
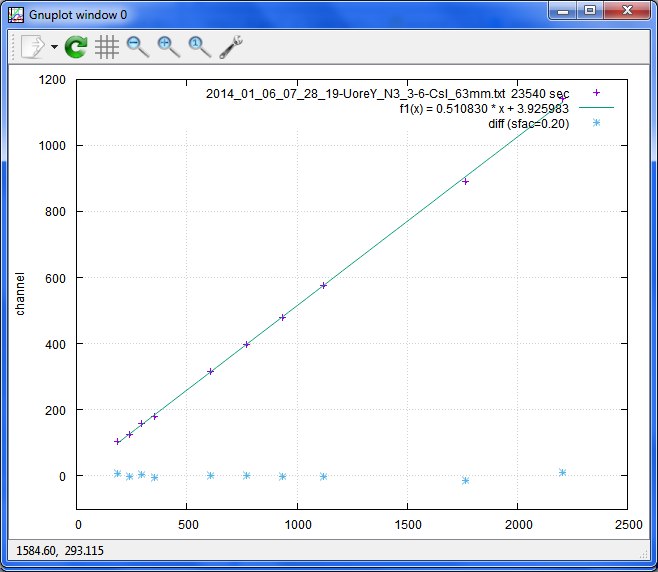
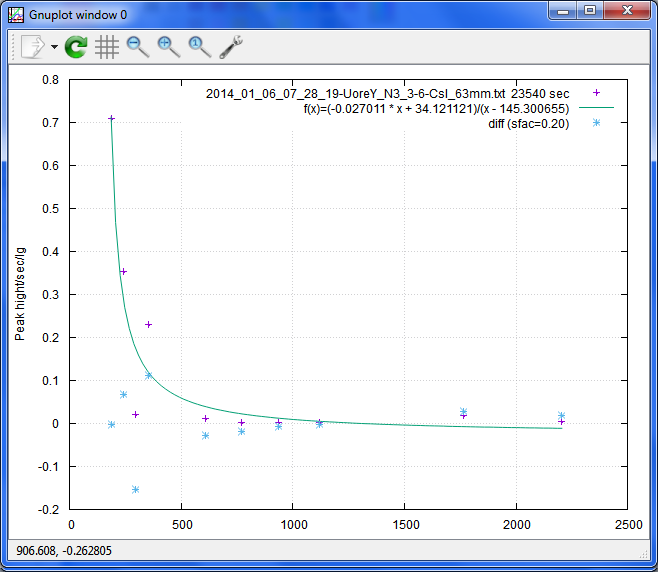
小さすぎで上手くいかなかった例 sfac=0.2:
エネルギー校正のフィットは、まずまずですが、効率曲線の方が駄目。
大きすぎて上手くいかなかった例 sfac=2, sfac=3:
2にすると、効率曲線がグダグダ
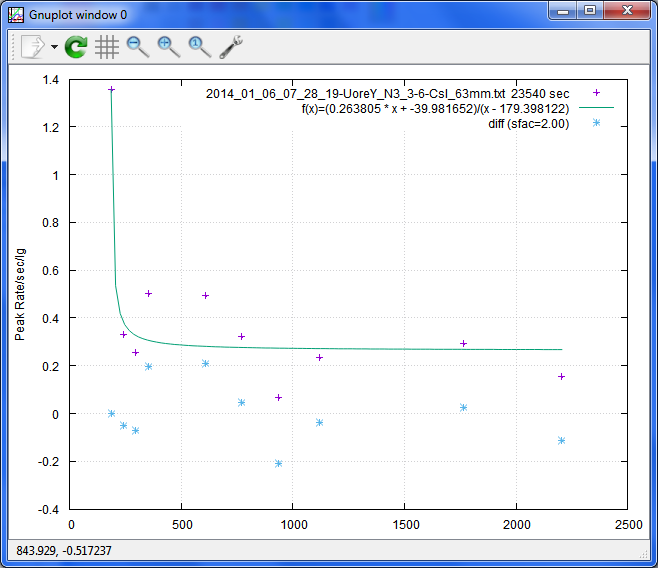
3だと、最後のピークで大きく失敗し、エネルギー校正も外れます。
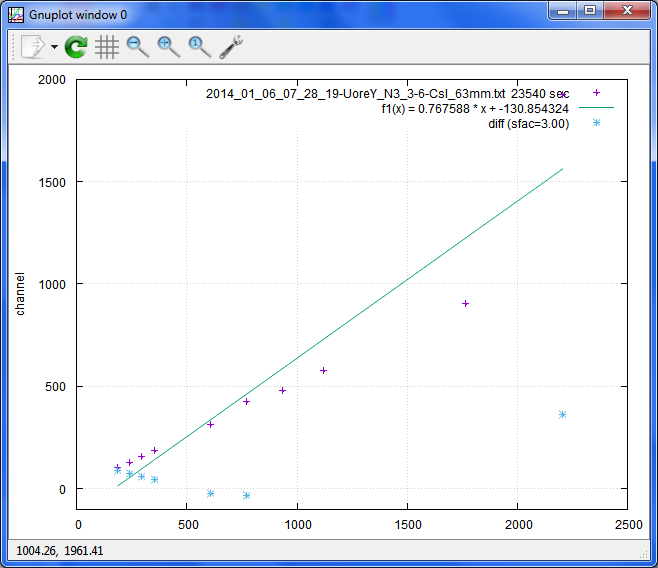
大体、0.8から1.5くらいの間でもって、まあまあのデータが取れるようです。
(手動で、一生懸命調整したのと同じ様な結果が自動的に得られます。)
ただし、まだ、いくつもの測定器のスペクトルでテストしたわけではないので、
分解能の違いなどによっては、上手くいかない可能性があります。
(初期値、というか、色々な設定は、標準的なNaI3インチに合わせてありますが、
どうにでも変更可能です。)