Peak Fit With Gnuplot Part4 検出器の特性調査編
Peak Fit With Gnuplot 最初の一歩とK40編、
Peak Fit With Gnuplot Part2 任意の単一ピーク編、
Peak Fit With Gnuplot Part3 複数ピーク+核種データ編の続編です。
他に、
Peak Fit With Gnuplot Part5 検出器の自動特性調査編、
Peak Fit With Gnuplot Part6 色々な関数編があります。
複数ピークのスクリプトの改造を進めるうちに、やっぱり色々なモデルを考える上で、
実際の検出器のデータ欲しい、ということで、まずウラン原石のスペクトルを利用して、
ピークを Peak Fit With Gnuplot Part2 で作ったスクリプトで調べてみました。
ウラン原石のスペクトルは、標準の3インチNaIをテレミノPMTアダプターに繋げて、去年測っておいたもの。
CsI63mmとファイル名に入っているのは、ノート欄の消し忘れだった筈。
http://pico.dreamhosters.com/raddata/2014_01_06_07_28_19-UoreY_N3_3-6-CsI_63mm.txt
これに対し、Identify.exeのライブラリーに登録してあるRa226のピークのエネルギーとその放出率のリストを使いました。
Ra226 A 1.60KY 186.11/3.280E 00 241.91/7.461E 00 295.09/1.917E 01 351.86/3.706E 01 609.31/4.609E 01 665.44/1.563E 00 768.34/4.885E 00 785.82/1.091E 00 806.15/1.229E 00 934.03/3.165E 00 1120.27/1.504E 01 1208.45/1.682E 01 1238.10/5.916E 00 1314.29/2.078E 01 1377.65/4.020E 00 1407.64/4.948E 00 1764.49/1.592E 01 1847.41/2.123E 00 2008.17/6.927E 00 2088.17/4.948E 00 2204.09/4.993E 00 2267.80/2.969E 00 2358.23/7.917E 00 2427.56/8.906E 00
まず、 Peak Fit With Gnuplot Part2 で作った、準備用スクリプトを走らせます。
http://pico.dreamhosters.com/raddata/ft0.plt
f='2014_01_06_07_28_19-UoreY_N3_3-6-CsI_63mm.txt'
load 'ft0.plt'
そして、上記のピークのエネルギーをEに代入しては、そのデータを調べて保存する、
というのを、この単一ピーク用スクリプトで、手動でやりました。
http://pico.dreamhosters.com/raddata/ft1.plt
n=3
E=186
@ft1
E=241
@ft1
という感じ。
なぜ、自動でやらなかったかといいますと、自動でやろうとしたら、上手くいかなかったからです。
これは、ピークによっては、隣と結構近いものもあり、調査の際のnの値を小さくしないと
良くフィットしないピークもあれば、逆に少し大きめにした方が、よいピークあるし、
全然フィットしないものもあったりした為です。
(もちろん、こういう作業も自動化しないと面倒ですから、将来的にはそうする予定です。)
その結果をコピペしたのがこれ。
http://pico.dreamhosters.com/raddata/Ra226_NaI_TPA_LC4.txt
そこから、調べたい部分を抜き出して、プロットしやすい形にしたのが、これ。
http://pico.dreamhosters.com/raddata/Ra226data.plt
上記のデータを使って、測定器の特性を調べます。
まず、ファイル名を扱いやすいように変数に入れます。
fr='Ra226data.plt'
フィットする直線と放物線を作ります。
fx1(x)=f1*x+f0
fx2(x)=f2*x**2+f1*x+f0
#適当に初期値を設定
f1=1
f0=1
f2=1
#最初は、エネルギーとチャンネルをフィット
fit fx1(x) fr u 1:3 via f1, f0
After 4 iterations the fit converged. final sum of squares of residuals : 10.6915 rel. change during last iteration : -1.29144e-008
degrees of freedom (FIT_NDF) : 8 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 1.15604 variance of residuals (reduced chisquare) = WSSR/ndf : 1.33644
Final set of parameters Asymptotic Standard Error ======================= ========================== f1 = 0.507544 +/- 0.0005654 (0.1114%) f0 = 6.3695 +/- 0.6027 (9.462%)
correlation matrix of the fit parameters: f1 f0 f1 1.000 f0 -0.795 1.000
f0が下駄で、f1が傾きですので、おおよそ1チャンネル当たり2keVになっています。
#結果をプロット
set xlabel 'Energy (keV)
set ylabel 'Channel'
plot fr u 1:3 t fr,fx1(x) t 'fit result'
見た目では、結構直線に乗ってます。

試しに、二次式でもフィット
fit fx2(x) fr u 1:3 via f2,f1,f0
After 9 iterations the fit converged. final sum of squares of residuals : 7.782 rel. change during last iteration : -1.64967e-012
degrees of freedom (FIT_NDF) : 7 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 1.05438 variance of residuals (reduced chisquare) = WSSR/ndf : 1.11171
Final set of parameters Asymptotic Standard Error ======================= ========================== f2 = 1.45643e-006 +/- 9.003e-007 (61.81%) f1 = 0.504214 +/- 0.002122 (0.4209%) f0 = 7.53665 +/- 0.907 (12.03%)
correlation matrix of the fit parameters: f2 f1 f0 f2 1.000 f1 -0.970 1.000 f0 0.795 -0.889 1.000
尻尾の上下の振れ方を決めるのがf2で、高いほうのデータが少ないせいか、正確でないせいか、
触れ幅が小さいからなのか、誤差が大きくなっています。
基本的な傾きを示すf1は、直線でフィットした時とあまり変わらず、誤差も小さくなっています。
下駄は、少し大きくなっています。
この例では、直線でもいいじゃないか?と思える結果ですが、気温とかの条件が変わると、
二次式の方が良いかもしれないので、直ぐに結論に飛びついて「確定しました」とか
思いたがらない方がよいでしょう。
#プロットしても、見た目には、直線とどこが違うのか?と思うような線。
plot fr u 1:3 t fr, fx2(x) t 'fx2'

次に、分解能の数値。
最初は、FWHMをエネルギーで表した場合。
fit fx1(x) fr u 1:4 via f1, f0
After 1 iterations the fit converged. final sum of squares of residuals : 190.697 rel. change during last iteration : -2.98082e-016
degrees of freedom (FIT_NDF) : 8 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 4.88233 variance of residuals (reduced chisquare) = WSSR/ndf : 23.8372
Final set of parameters Asymptotic Standard Error ======================= ========================== f1 = 0.0538021 +/- 0.002388 (4.438%) f0 = 11.663 +/- 2.545 (21.82%)
correlation matrix of the fit parameters: f1 f0 f1 1.000 f0 -0.795 1.000
縦軸のラベルを変えてプロット。
直線からは、ちょっと外れている様な気がします・・・
set ylabel 'FWHM (keV)'
plot fr u 1:4 t fr,fx1(x) t 'fit result'

二次式でフィット
fit fx2(x) fr u 1:4 via f2,f1,f0
After 5 iterations the fit converged. final sum of squares of residuals : 7.782 rel. change during last iteration : -2.76913e-007
degrees of freedom (FIT_NDF) : 7 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 1.05438 variance of residuals (reduced chisquare) = WSSR/ndf : 1.11171
Final set of parameters Asymptotic Standard Error ======================= ========================== f2 = 1.45643e-006 +/- 9.003e-007 (61.81%) f1 = 0.504214 +/- 0.002122 (0.4209%) f0 = 7.53665 +/- 0.907 (12.03%)
correlation matrix of the fit parameters: f2 f1 f0 f2 1.000 f1 -0.970 1.000 f0 0.795 -0.889 1.000
あまり代わり映えしませんし、高い方が線から外れている様な気がします。
plot fr u 1:4 t fr, fx2(x) t 'fit result'

そこで、1000keV以下についてフィットさせてみました。
fit [0:1000] fx2(x) fr u 1:4 via f2,f1,f0
After 5 iterations the fit converged. final sum of squares of residuals : 4.84629 rel. change during last iteration : -8.55987e-006
degrees of freedom (FIT_NDF) : 4 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 1.10072 variance of residuals (reduced chisquare) = WSSR/ndf : 1.21157
Final set of parameters Asymptotic Standard Error ======================= ========================== f2 = -8.85315e-006 +/- 8.654e-006 (97.75%) f1 = 0.0764678 +/- 0.009656 (12.63%) f0 = 4.73412 +/- 2.147 (45.36%)
correlation matrix of the fit parameters: f2 f1 f0 f2 1.000 f1 -0.987 1.000 f0 0.916 -0.961 1.000
プロットでは、1000keV以降も出してみると、こっちの方が、高いほうの一部を除き、
合っているんじゃないか?とか思えますが、たった一つの測定データですので、
まだ良く分かりません。
あ、それと、そもそも、2次式に当てはまるようなものなのか、それとも平方根なのか、とか、
そういう話もありますので、基礎的な理屈を確認せずに、単純にどんな風な分布になるか
見ているだけの段階です。
plot fr u 1:4 t fr, fx2(x) t 'fit result'

続いて、FWHMをパーセントで出した値。
これは、エネルギーで出した値をエネルギーで割っているので、上のものとは、違う結果になる筈。
fit fx1(x) fr u 1:5 via f1,f0
After 5 iterations the fit converged. final sum of squares of residuals : 3.83942 rel. change during last iteration : -4.97362e-014
degrees of freedom (FIT_NDF) : 8 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.692768 variance of residuals (reduced chisquare) = WSSR/ndf : 0.479928
Final set of parameters Asymptotic Standard Error ======================= ========================== f1 = -0.00197559 +/- 0.0003388 (17.15%) f0 = 9.45041 +/- 0.3612 (3.822%)
correlation matrix of the fit parameters: f1 f0 f1 1.000 f0 -0.795 1.000
set ylabel 'FWHM (%)'
plot fr u 1:5 t fr, fx1(x) t 'fit result'
まあ、分解能が、エネルギーが高くなるに連れて、よくなっていく(小さい値になっていく)というのは、わかりますが、
結構ばらついている感じ。
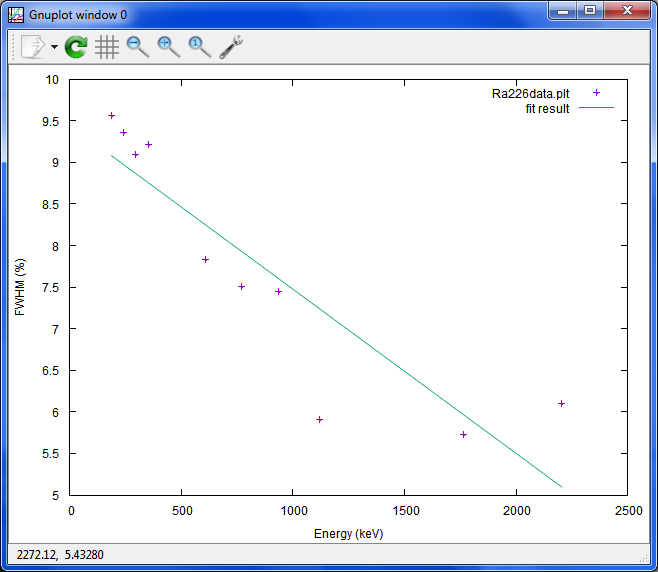
fit fx2(x) fr u 1:5 via f2,f1,f0
After 5 iterations the fit converged. final sum of squares of residuals : 0.752157 rel. change during last iteration : -6.55723e-009
degrees of freedom (FIT_NDF) : 7 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.327797 variance of residuals (reduced chisquare) = WSSR/ndf : 0.107451
Final set of parameters Asymptotic Standard Error ======================= ========================== f2 = 1.50026e-006 +/- 2.799e-007 (18.66%) f1 = -0.00540577 +/- 0.0006597 (12.2%) f0 = 10.6527 +/- 0.282 (2.647%)
correlation matrix of the fit parameters: f2 f1 f0 f2 1.000 f1 -0.970 1.000 f0 0.795 -0.889 1.000
plot fr u 1:5 t fr, fx2(x) t 'fit result'
二次式の方も、高いほうで、分解能が悪化し始めるような線を引いているし、
エネルギーとチャンネルの関係の様に、簡単にいきません。

次は、効率曲線。これが、お目当てです。
この場合、ピークの山の高さを測定秒数で割ってレートにし、それを放出率で割っています。
直線にはならないのは分かっているのですが、まずは、直線で試してみます。
set ylabel 'Rate / Intensity (ratio)'
fit fx1(x) fr u 1:($6/$2) via f1,f0
After 4 iterations the fit converged. final sum of squares of residuals : 0.0183549 rel. change during last iteration : -3.51153e-007
degrees of freedom (FIT_NDF) : 8 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.0478995 variance of residuals (reduced chisquare) = WSSR/ndf : 0.00229436
Final set of parameters Asymptotic Standard Error ======================= ========================== f1 = -5.15391e-005 +/- 2.343e-005 (45.45%) f0 = 0.085851 +/- 0.02497 (29.09%)
correlation matrix of the fit parameters: f1 f0 f1 1.000 f0 -0.795 1.000
plot fr u 1:($6/$2) t fr, fx1(x) t 'fit result'
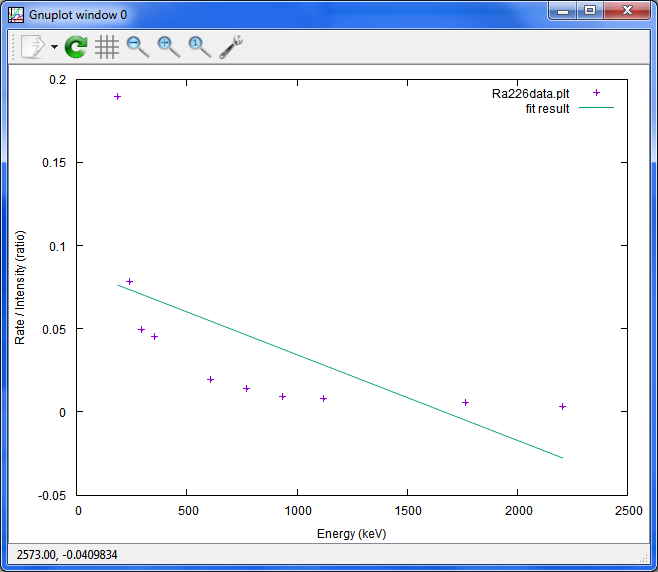
こういう式だとうまくフィットするという例がありましたので、それで試してみます。
f(x)=(a*x+b)/(x-c)
a=0.0001
b=50
c=50
fit f(x) fr u 1:($6/$2) via a,b,c
After 14 iterations the fit converged. final sum of squares of residuals : 6.95851e-005 rel. change during last iteration : -2.21749e-008
degrees of freedom (FIT_NDF) : 7 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.00315289 variance of residuals (reduced chisquare) = WSSR/ndf : 9.94073e-006
Final set of parameters Asymptotic Standard Error ======================= ========================== a = 0.00108725 +/- 0.00164 (150.8%) b = 7.52324 +/- 0.7245 (9.63%) c = 145.242 +/- 2.732 (1.881%)
correlation matrix of the fit parameters: a b c a 1.000 b -0.874 1.000 c 0.647 -0.917 1.000
plot fr u 1:($6/$2) t fr, f(x) t 'fit result'
こんな感じでもいいのかも。
でも、a の誤差が大きいのが気になる。

aの初期値を a=0.00000001 という風にしてみたら、
fit f(x) fr u 1:($6/$2) via a,b,c
After 4 iterations the fit converged. final sum of squares of residuals : 7.38823e-005 rel. change during last iteration : -9.22346e-007
degrees of freedom (FIT_NDF) : 7 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.00324879 variance of residuals (reduced chisquare) = WSSR/ndf : 1.05546e-005
Final set of parameters Asymptotic Standard Error ======================= ========================== a = 1.00243e-008 +/- 0.001698 (1.694e+007%) b = 7.94798 +/- 0.7552 (9.501%) c = 144.035 +/- 2.866 (1.99%)
correlation matrix of the fit parameters: a b c a 1.000 b -0.874 1.000 c 0.647 -0.917 1.000
プロットの結果をみても見た目には違いが分からないし、
なんか、a の値って、あんまり重要ではないみたい・・・
続いて、山の高さだけでなく、それと分解能で決まる山の面積のレートでもってやってみます。
fit f(x) fr u 1:($7/$2) via a,b,c
After 24 iterations the fit converged. final sum of squares of residuals : 0.0426616 rel. change during last iteration : -4.59772e-009
degrees of freedom (FIT_NDF) : 7 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.0780674 variance of residuals (reduced chisquare) = WSSR/ndf : 0.00609451
Final set of parameters Asymptotic Standard Error ======================= ========================== a = 0.259167 +/- 0.04281 (16.52%) b = 49.9732 +/- 23.45 (46.94%) c = 132.19 +/- 10.27 (7.767%)
correlation matrix of the fit parameters: a b c a 1.000 b -0.849 1.000 c 0.657 -0.940 1.000
plot fr u 1:($7/$2) t fr, f(x) t 'fit result'
こちらの方がバラツキが少し大きいですが、多分、分解能の数値のばらつきのせいでしょう。

つづきは、自動特性調査編