Peak Fit With Gnuplot Part6 色々な関数編
Peak Fit With Gnuplot 最初の一歩とK40編、
Peak Fit With Gnuplot Part2 任意の単一ピーク編、
Peak Fit With Gnuplot Part3 複数ピーク+核種データ編、
Peak Fit With Gnuplot Part4 検出器の特性調査編、
Peak Fit With Gnuplot Part5 検出器の自動特性調査編の続編です。
次は、
Peak Fit With Gnuplot Part7 実用的なスクリプトの実験。
Gnuplotの色々な使い方は、以下のページに書いてあります。
Gnuplot Memo
Gnuplot Memo3D
Gnuplot Memo2
私の目標は、まず、私が使っているNaI3インチの測定器の応答関数をでっち上げることで、
それを使って、色々な核種のピークをフィットすることです。
で、その手始めに、K40のピークを使って色々やったり、Ra226やEu152などで、
測定器の各種特性を調べたりしているわけですが、
肝心の応答関数の方は、コンプトンたんは、一応良さそうで、コンプトン丘も三次関数で良さそうなのですが、
430keV以下のエネルギーの低い方や、バックスキャッターの取り扱い、
そして、さらには200keVより下の方の扱いなどで悩んでいるところです。
で、悩んでいる理由は、応答関数を作るのに、どういう曲線を使うと
メインピークに連動させるのが楽で、
Gnuplotが楽に計算できて、
フィットが収束しやすいか、
という、基礎知識が圧倒的に欠けているので、
まず、色々な関数と曲線の例をこのところ(というか、かなり前から)眺めたり、
プロットしたり、フィットしたりして試しながら学習しているところです。
そういうわけで、このページは、そういう、色々な関数のメモのページです。
このページや、
http://www.lightstone.co.jp/origin/flist6.html
このページなどが、非常に参考になります。
https://www.hulinks.co.jp/software/peakfit/functions.html
ガウス関数のおさらい
ガウス関数と言っても、ピークの高さに着目した形、面積に着目した形、
統計の様に、面積が常に1になるように正規化したもの、などなどがあります。
で、私が今のところ良く使っているのは、高さに着目した形です。
これは、y=0の線の上の、エネルギーがEの位置に、高さがhで、幅(というか太り方)がs(シグマ)の
ガウス曲線を出す関数です。*は、掛け算で、**2はGnuplotやPythonでの二乗の書き方です。
g(x)=h*exp(-(x-E)**2/(2*s**2))
計算機に、もう少し優しい形にすると、こうでしょうか。
g1(x)=h*exp(-0.5*((x-E)/s)**2)
変数でなく、引数で、パラメーターを指定するなら、こうすればよいだけ。
gg(x,h,E,s)=h*exp(-0.5*((x-E)/s)**2)
高さを1、中心のエネルギーがゼロ、シグマが1でプロットすると、こうなります。
h=1;E=0;s=1
reset;unset xr;unset yr
set title 'h=1;E=0;s=1'
plot g1(x) t 'g1(x)=h*exp(-0.5*((x-E)/s))**2)'
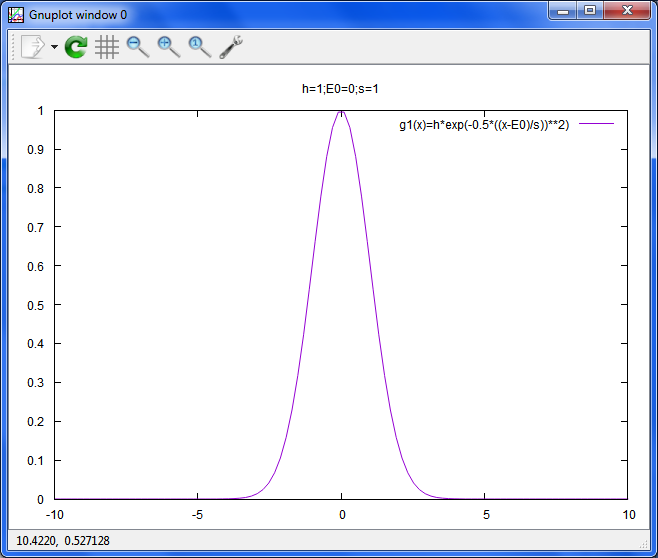
ガウス関数では、FWHM(半値幅)が良く出てきて、それは、シグマと定数で簡単に出せます。
fwhm=s*2*sqrt(2*log(2))
この部分は、定数なので、一度計算して、変数に入れておくと、それ以降、Gnuplotは計算しないで済みます。
s2fwhm=2*sqrt(2*log(2))
fwhm=s*s2fwhm
このFWHMは、keVの値で、よくある%の値にしたい時は、ピークのエネルギーEで割って、100をかけます。
Pfwhm=fwhm/E*100
また、面積(Np)は、s(シグマ)に√2πと高さをかければ良いので、簡単。
Np=h*sqrt(2*pi)*s
で、√2πも定数なので、こうしておくとGnuplotは少し楽。
rt2pi=sqrt(2*pi)
Np=h*rt2pi*s
後は、中央から、両側にsの分だけの面積は、全体の約68%で、2sだと約95%で、3sだと約99.7%というのは、
統計で使うガウス曲線(正規分布)と同じなので、おぼえておくと、便利な場合があります。
このガウス曲線をy=b、傾きがaの直線の上に乗せたい時には、こんな風にするだけ。
要は、混ぜたい線を足してやれば良いだけです。
g2(x)=h*exp(-0.5*((x-E)/s)**2)+a*(x-E)+b
a=0.5;b=2
set title 'h=1;E=0;s=1;a=0.5;b=2'
plot g2(x) t 'g2(x)=h*exp(-0.5*((x-E)/s))**2)+a*(x-E)+b',g1(x),a*(x-E)+b
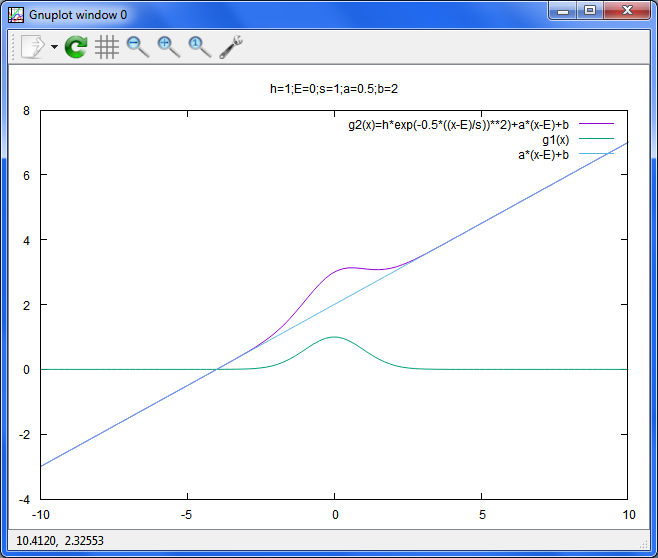
二次曲線や三次曲線に乗せても良いですし、まあ、なんでも好きに試してみると良いでしょう。
参考ページの式やグラフィック (これら二つは、y0があるかどうかを除くと、同じものですが、変数の名前が違っています。):
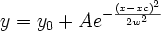
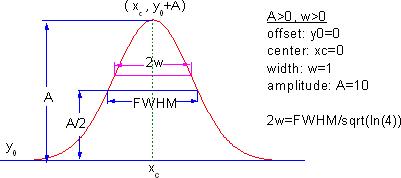
Gaussian (Amplitude) https://www.hulinks.co.jp/software/peakfit/functions.html

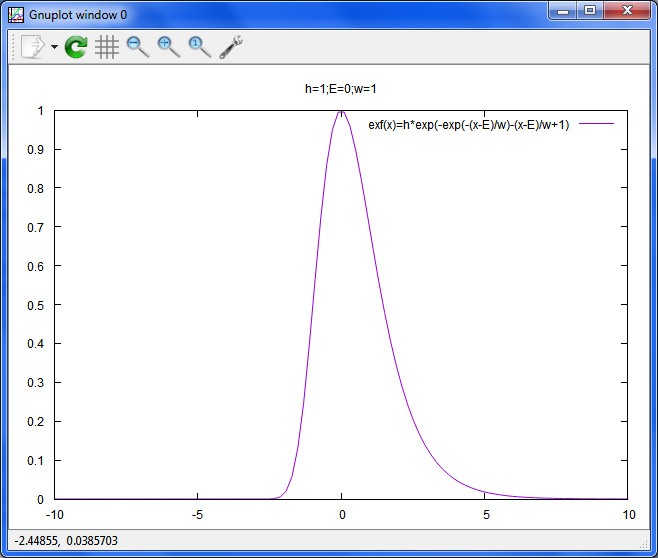
エクストリーム関数(極値分布)
reset;unset xr;unset yrset title 'h=1;E=0;w=1'
h=1;E=0;w=1
exf(x)=h*exp(-exp(-(x-E)/w)-(x-E)/w+1)
plot exf(x) t 'exf(x)=h*exp(-exp(-(x-E)/w)-(x-E)/w+1)'
引数指定形式
exfg(x,h,E,w)=h*exp(-exp(-(x-E)/w)-(x-E)/w+1)
バックグラウンドと一緒に出して、様子を見ています。
h=0.16
E=175
w=200
set title sprintf('h=%f, E=%d, w=%f',h,E,w)
plot [0:2600] exf(x), f every ::HL::BGL u 1:($2/sec) with dot

Extreme:統計分野で使われるExtreme関数 http://www.lightstone.co.jp/origin/flist6.html
Extreme Value (Amplitude) https://www.hulinks.co.jp/software/peakfit/functions.html

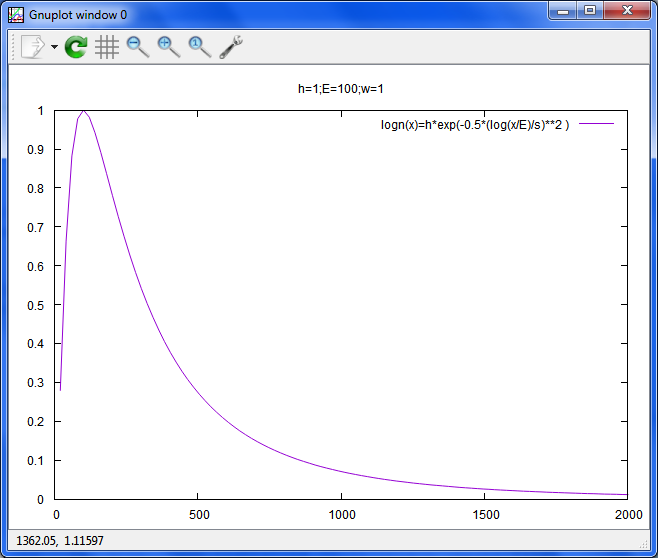
LogNorm
reset;unset xr;unset yrset title 'h=1;E=100;w=1'
h=1;E=100;w=1
logn(x)=h*exp(-0.5*(log(x/E)/s)**2 )
plot [0:2000] logn(x) t 'logn(x)=h*exp(-0.5*(log(x/E)/s)**2 )'
引数指定形式
logng(x,h,E,s)=h*exp(-0.5*(log(x/E)/s)**2 )
h=0.17;E=160;s=0.85
set title 'h=0.17;E=160;s=0.85'
plot [0:2000] logn(x) t 'logn(x)=h*exp(-0.5*(log(x/E)/s)**2 )',f every ::HL::BGL u 1:($
2/sec) with dot
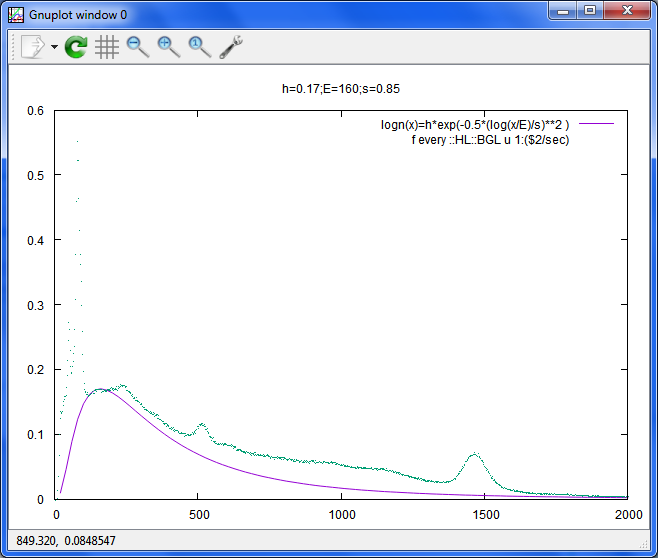
エクストリーム関数も(引数指定形式で)追加して、比較。
plot [0:2000] logn(x) t 'logn(x)=h*exp(-0.5*(log(x/E)/s)**2 )',f every ::HL::BGL u 1:($
2/sec) with dot,exfg(x,0.17,160,120)
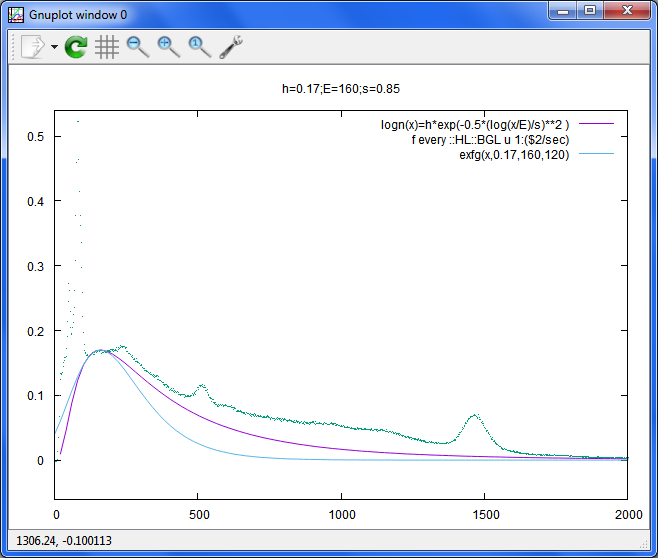
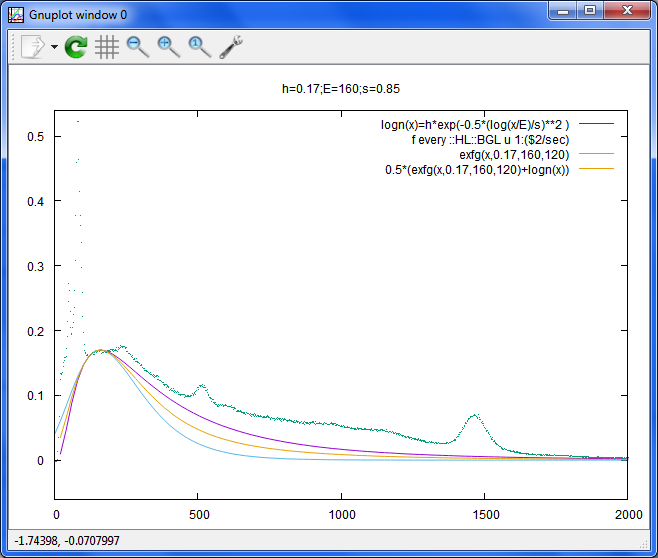
二つを足して2で割って、平均化
plot [0:2000] logn(x) t 'logn(x)=h*exp(-0.5*(log(x/E)/s)**2 )',f every ::HL::BGL u 1:($
2/sec) with dot,exfg(x,0.17,160,120),0.5*(exfg(x,0.17,160,120)+logn(x))
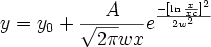
Log Nomal (Amplitude)

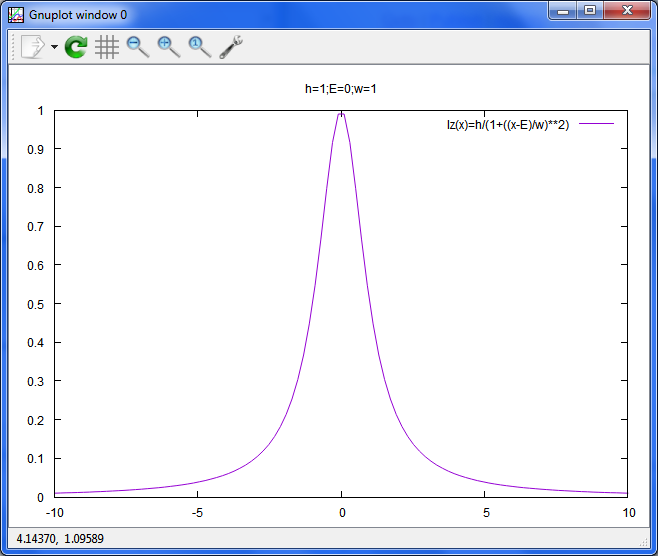
ローレンツピーク
reset;unset xr;unset yr
set title 'h=1;E=0;w=1'
h=1;E=0;w=1
lz(x)=h/(1+((x-E)/w)**2)
plot lz(x) t 'lz(x)=h/(1+((x-E)/w)**2)'
引数指定形式
lz(x,h,E,w)=h/(1+((x-E)/w)**2)
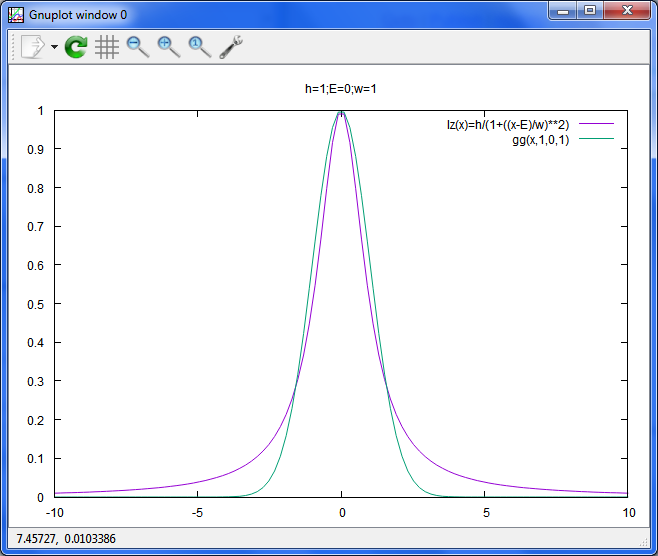
ガウス曲線との比較
plot lz(x) t 'lz(x)=h/(1+((x-E)/w)**2)',gg(x,1,0,1)
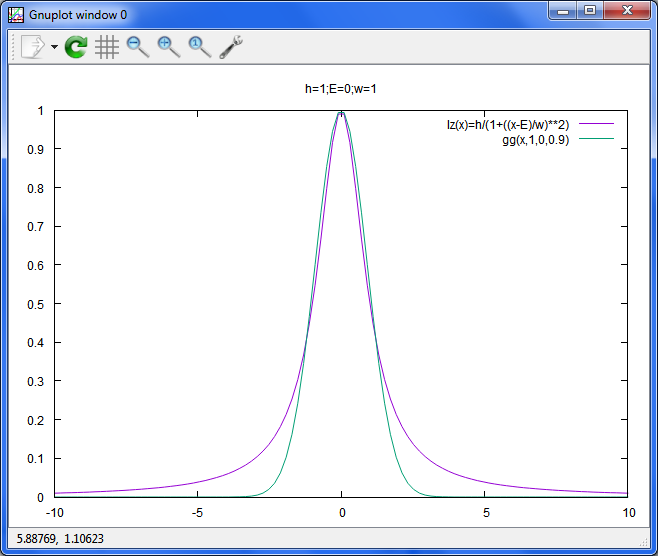
ガウス曲線を1割痩せさせて比較。
plot lz(x) t 'lz(x)=h/(1+((x-E)/w)**2)',gg(x,1,0,0.9)
ピークの形状によっては、二つを適当に混ぜたり、左右で組み合わせたり、片側だけ混ぜたり、
左右違う割合で混ぜたり、まあ、色々なことが出来そう。
参考ページ(ただし、二つの式が入れ替わっている場所があるので要注意)
http://www.nanophoton.jp/techniques/analysis02.html
Lorentz:ローレンツピーク関数
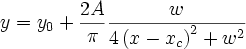
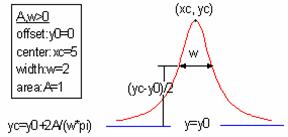
Lorentzian (Amplitude)

いちおう、こういうのも書いておきます。
直線
ごくフツーの形
f(x)=a*x+b
エネルギーがEで、高さbの点を通る、傾きがaの直線。
f(x)=a*(x-E)+b
二次式(放物線)
ごくフツーの形
f(x)=a*x**2+b*x+c
エネルギーがEで、高さbの点を通る、縦長の度合いがaの放物線。
f(x)=a*(x-E)**2+b
平方根
f(x)=sqrt(x)
(E,b)から上に出る、平方根の線
f(x)=a*sqrt(x-E)+b
Gnuplotに入っている関数
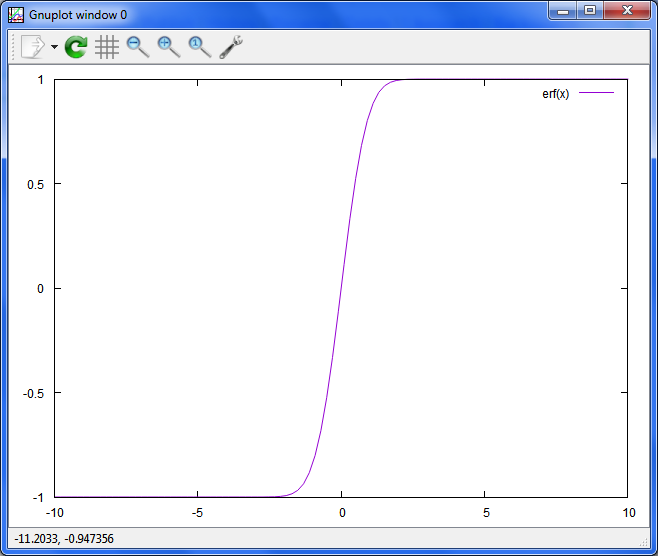
xの実部の誤差関数
plot erf(x)
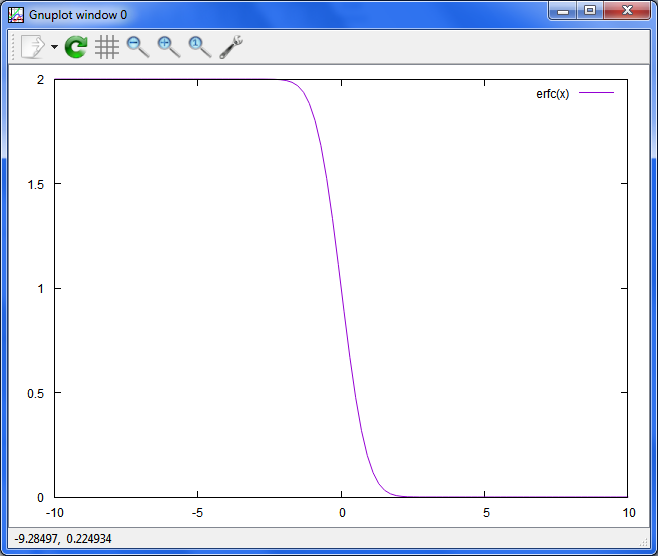
1 - xの誤差関数
plot erfc(x)
xの実部の逆誤差関数
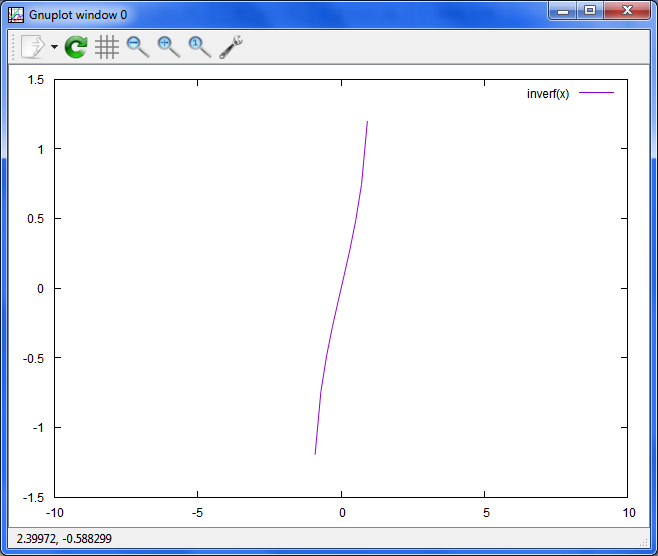
plot inverf(x)
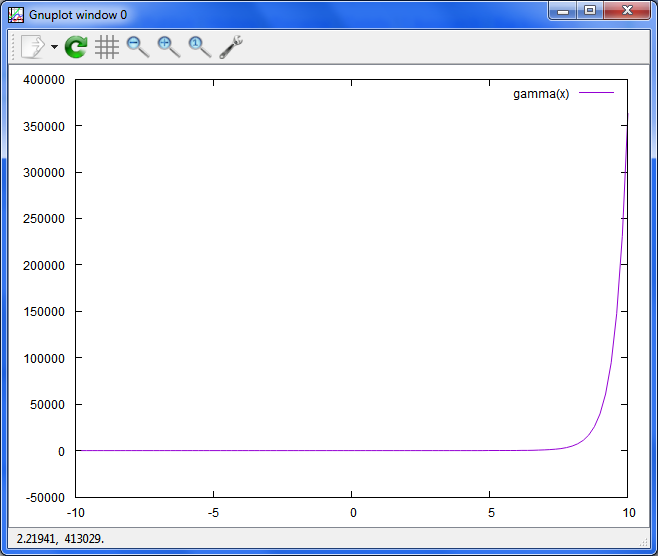
xの実部のガンマ関数
plot gamma(x)
あれ?エラーが出ます。xは、任意で良いと、書いてあったのに、違うのかな?分からないので、パス。グラフは、一応出てますが。
lngamma singularity error
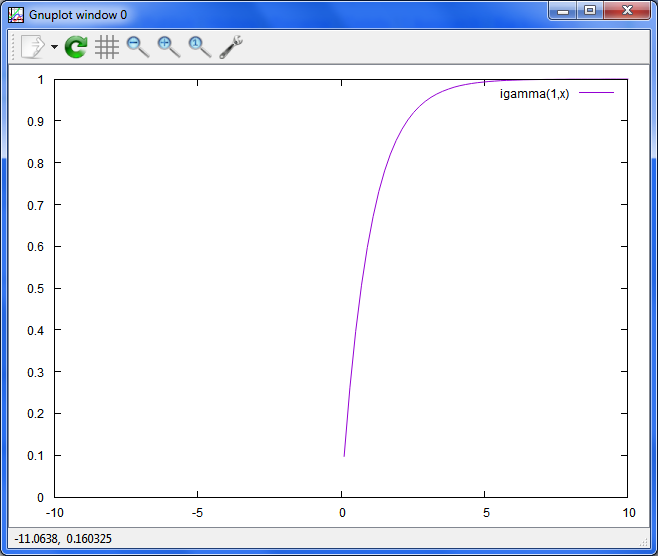
a, xの実部の不完全ガンマ関数
plot igamma(1,x)
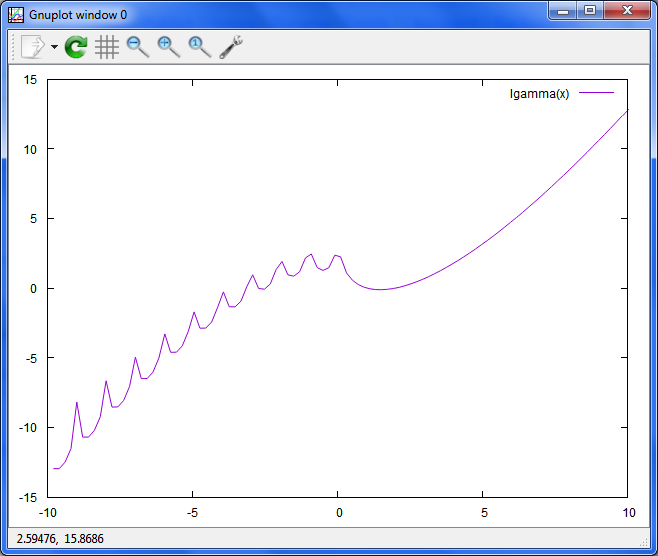
xの実部のガンマ対数関数
plot lgamma(x)
これもエラーが出ますが、ファンキーなグラフが出ます。
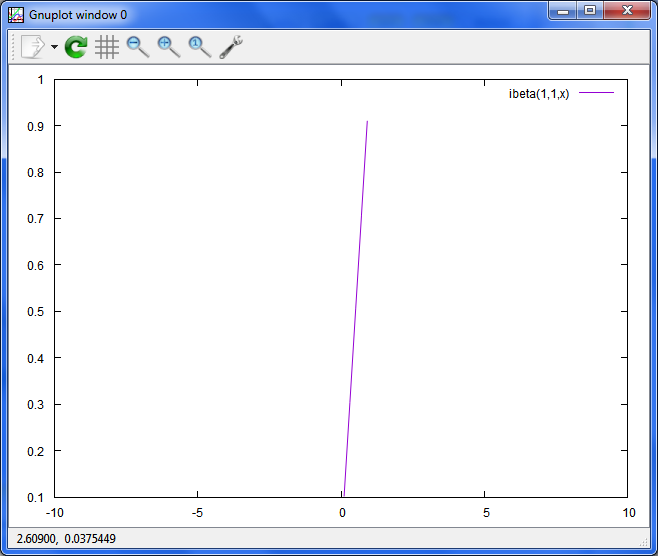
xの実部の不完全ベータ関数
plot ibeta(1,1,x)
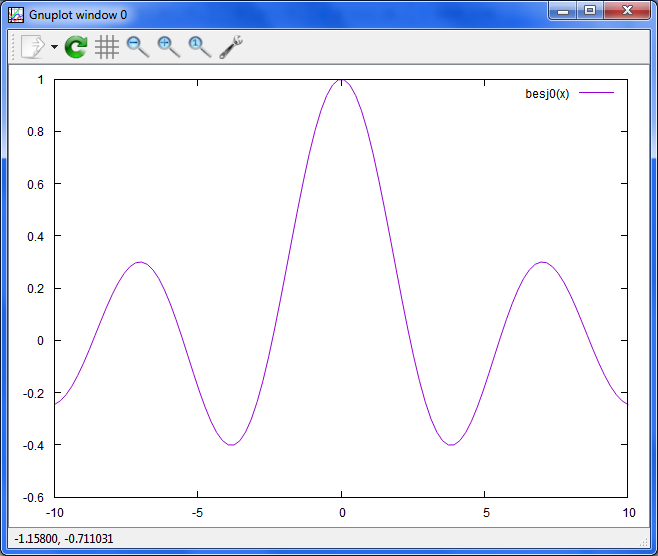
xのj0次ベッセル関数
plot besj0(x)
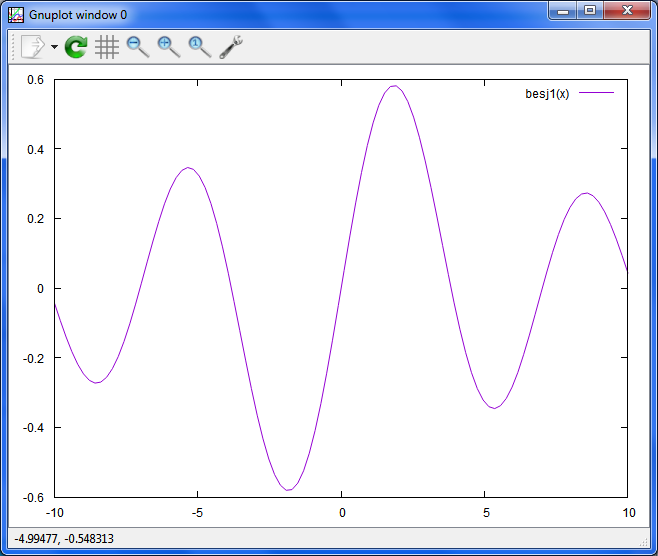
xのj1次ベッセル関数
plot besj1(x)
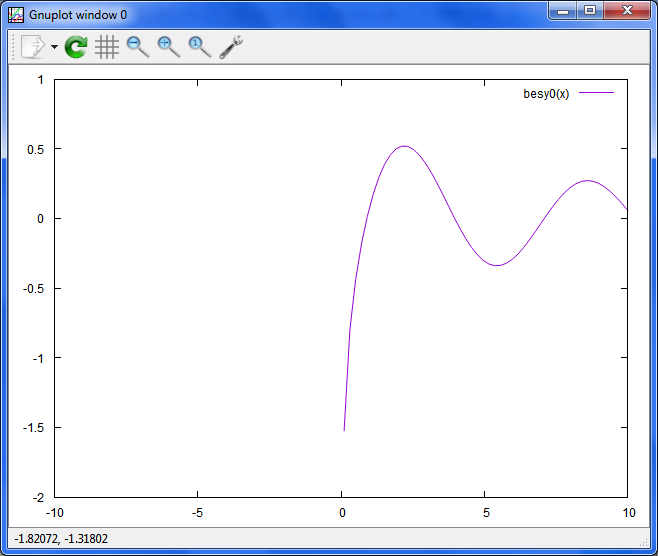
xのy0次ベッセル関数
plot besy0(x)
xのy1次ベッセル関数
plot besy1(x)
xの実部の正規分布(ガウス分布 関数
ガウス曲線を積分した形
plot norm(x)
xの実部の逆正規分布関数
plot invnorm(x)
ランベルトのW関数
plot lambertw(x)
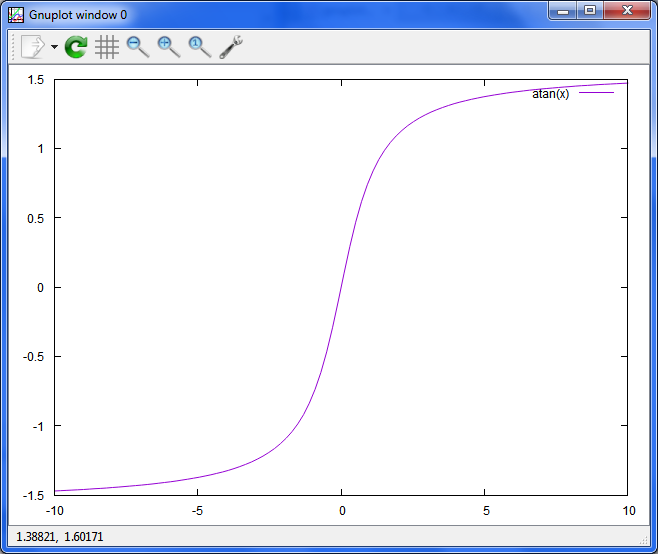
xの逆正接(アークタンジェント)
plot atan(x)
xの逆双曲線正弦
plot asinh(x)

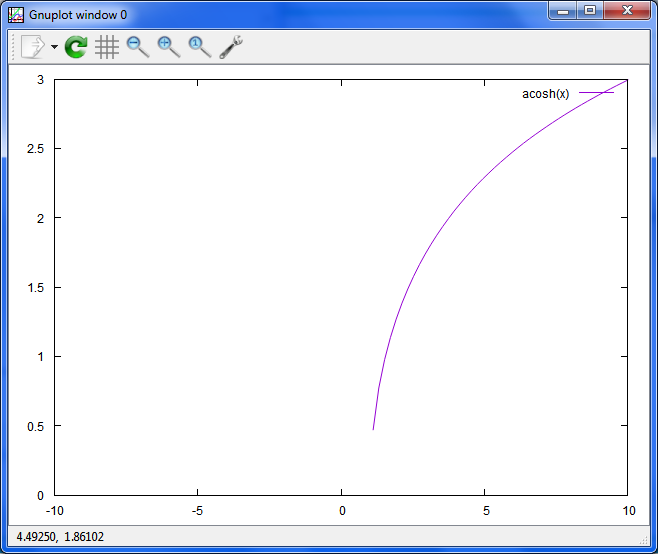
xの逆双曲線余弦
plot acosh(x)
xの逆双曲線正接
plot atanh(x)

Gnuplotに入っている関数は、ここにもリストがあります。
http://www5a.biglobe.ne.jp/~nkgwtty/nn_gnuplot2.html
また、こちらのページも、みんなサンプルや画像付きで、Gnuplotの色々な点が分かりやすいです。
http://www5a.biglobe.ne.jp/~nkgwtty/nn_gnuplot.html
後は、ここに使えるかもしれない関数があります。
http://gnuplot.sourceforge.net/demo_cvs/spline.html
Peak Fit With Gnuplot Part7 応答関数の低い方のテストです。