Date: 2015/04/07 10:08(22) --- Name: nkom
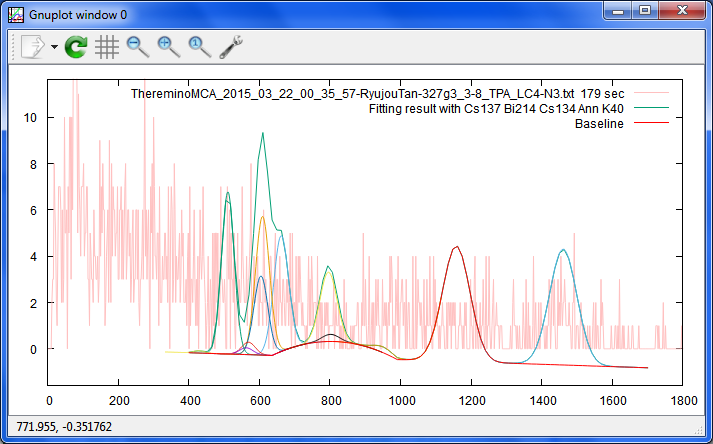
さすがに、179秒の測定だと、完全に失敗しています。
「K40のピークだけ」を先にフィットしておいて、それを固定した形で残りをやった方が良いのかも。
After 37 iterations the fit converged.
final sum of squares of residuals : 3435.33
rel. change during last iteration : -6.92255e-006
degrees of freedom (FIT_NDF) : 608
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 2.37702
variance of residuals (reduced chisquare) = WSSR/ndf : 5.65021
Final set of parameters Asymptotic Standard Error
======================= ==========================
hEc = 4.99535 +/- 0.5203 (10.42%)
sEc = 38.8443 +/- 4.887 (12.58%)
b0 = 0.0330261 +/- 0.4513 (1366%)
b1 = -0.000499926 +/- 0.000355 (71.02%)
cb0 = -2.19872e-005 +/- 3.088e-005 (140.4%)
cbx = 813.53 +/- 64.07 (7.876%)
cby = 0.689609 +/- 0.4188 (60.72%)
hCs137_1 = 4.99777 +/- 1.175 (23.51%)
hBi214_1 = 5.98872 +/- 1.004 (16.76%)
hCs134_1 = 2.98926 +/- 0.6301 (21.08%)
hAnn_1 = 6.99607 +/- 0.7325 (10.47%)
hK40_1 = 4.99732 +/- 0.491 (9.826%)
correlation matrix of the fit parameters:
hEc sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
hEc 1.000
sEc -0.449 1.000
b0 -0.090 -0.149 1.000
b1 0.016 0.026 -0.936 1.000
cb0 -0.001 -0.001 -0.013 0.016 1.000
cbx 0.006 0.009 0.059 -0.075 -0.460 1.000
cby 0.077 0.128 -0.364 0.261 -0.647 0.042 1.000
hCs137_1 0.006 0.010 -0.033 0.025 -0.629 0.764 0.119 1.000
hBi214_1 0.033 0.055 -0.215 0.177 -0.258 -0.154 0.557 -0.165 1.000
hCs134_1 0.019 0.031 -0.135 0.115 0.407 0.083 -0.544 0.060 -0.734 1.000
hAnn_1 0.072 0.120 -0.539 0.462 -0.005 -0.027 0.240 0.018 0.144 0.051 1.000
hK40_1 0.095 0.157 0.091 -0.270 -0.018 0.022 0.086 0.008 0.018 0.005 0.015 1.000
9.60117535958298e-006, -2.19872381903652e-005, -4.08646109812452
9.60117535958298e-006, -2.19872381903652e-005, -4.08646109812452
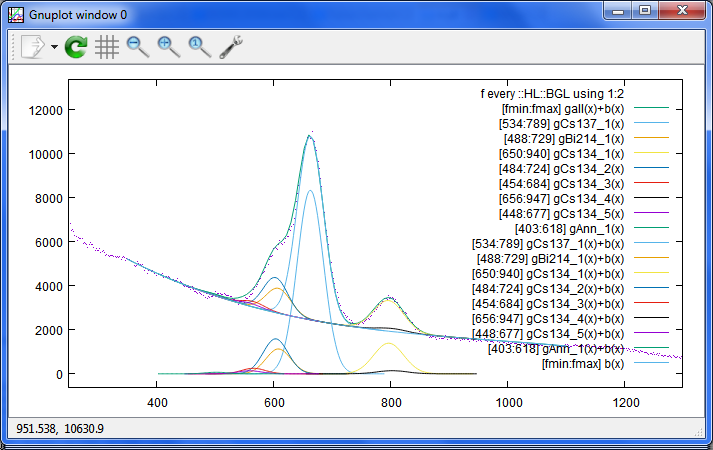
Date: 2015/04/07 09:51(54) --- Name: nkom
この方法の楽な点は、スムージングを考えなくて良いというところです。
関数でまとめて比較するので、事前に特に何にもしないで、スクリプトを走らせるだけ。
タイトルにファイル名と測定秒数を出す様にして、一々全部のピークの凡例を出すのは止めました。
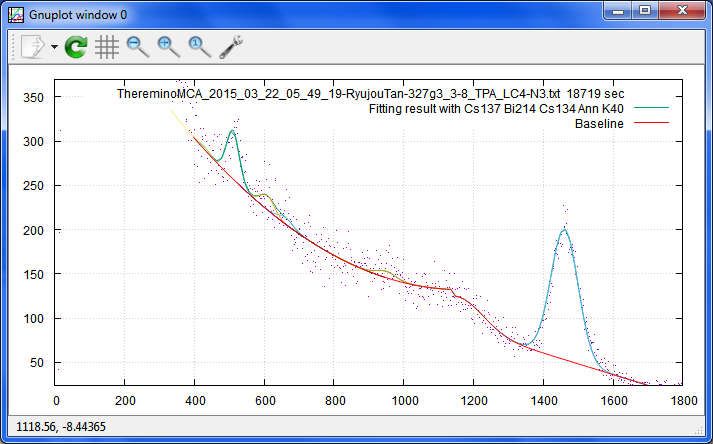
これは、粒状炭を5時間測ったスペクトルですが、Cs137は目で見ても、数値的にも、
「検出」と言えるほどの確かさは、まだ無いでしょう。
After 17 iterations the fit converged.
final sum of squares of residuals : 101114
rel. change during last iteration : -4.66684e-006
degrees of freedom (FIT_NDF) : 608
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 12.896
variance of residuals (reduced chisquare) = WSSR/ndf : 166.306
Final set of parameters Asymptotic Standard Error
======================= ==========================
hEc = 34.1427 +/- 4.618 (13.53%)
sEc = 70.94 +/- 10.29 (14.51%)
b0 = 230.382 +/- 16.98 (7.37%)
b1 = -0.121436 +/- 0.01086 (8.945%)
cb0 = 0.000293924 +/- 1.973e-005 (6.713%)
cbx = 956.747 +/- 23.47 (2.453%)
cby = 30.4468 +/- 6.721 (22.07%)
hCs137_1 = 7.39989 +/- 3.668 (49.57%)
hBi214_1 = 16.171 +/- 4.567 (28.24%)
hCs134_1 = 0.0932504 +/- 3.14 (3367%)
hAnn_1 = 54.7814 +/- 3.937 (7.187%)
hK40_1 = 147.605 +/- 3.208 (2.173%)
correlation matrix of the fit parameters:
hEc sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
hEc 1.000
sEc 0.437 1.000
b0 -0.822 -0.705 1.000
b1 0.809 0.682 -0.997 1.000
cb0 0.004 0.004 -0.004 0.004 1.000
cbx 0.634 0.535 -0.783 0.785 -0.554 1.000
cby 0.824 0.724 -0.981 0.970 -0.063 0.783 1.000
hCs137_1 0.007 0.007 -0.007 0.006 0.374 -0.262 -0.045 1.000
hBi214_1 -0.003 -0.003 0.003 -0.002 -0.219 0.087 0.032 -0.237 1.000
hCs134_1 0.008 0.008 -0.008 0.008 0.465 -0.290 -0.064 0.361 -0.643 1.000
hAnn_1 0.005 0.005 -0.005 0.004 -0.026 -0.102 -0.006 0.180 0.043 0.151 1.000
hK40_1 0.488 0.489 -0.494 0.454 0.009 0.353 0.539 0.014 -0.005 0.017 0.010 1.000
9.60117535958298e-006, 0.000293924106664719, -4.08646109812452
9.60117535958298e-006, 0.000313592070357552, -4.08646109812452
Date: 2015/04/07 08:56(43) --- Name: nkom
しかし、この先も長いです。
応答関数もどきが出来たら、K40の線量の違う検体を測って、
光電ピークと、応答関数の具材のパラメーターの関係を
適当な関数で見繕わないとならないし。
そしたら、今度はその上でセシウム137を混ぜて、
セシウム137のコンプトン散乱のパラメータを調べます。
素人測定的には、後は、ウラン系とトリウム系、
そしてBe7を混ぜて、トンテモない酷い結果を出さないのを確認したり、
不検出の認識や表示の問題とか、検出時のカウント数やら
効率曲線とかから線量への計算などがあります。
後は、セシウム134が多い場合に、K40にサムピークやらが
被さってくるわけで、それもサブピークの一つとして扱いながら、
高さはGnuplotにお任せでFitして貰えるのかどうか、とか、
細かな点はやろうとすると、とっても沢山あるのでしょうが、
まずは、あんまり細かいところは無視して、
「見えてるピークを取りこぼさない」というのと、
「ありもしないピークを見つけてしまわない」という点に合格するのが第一。
人間でも、出来てない場合があるわけですから、
堅物のGnuplotさんにやってもらうには、スクリプトの方で
あれこれお世話をしてあげないとなりません。
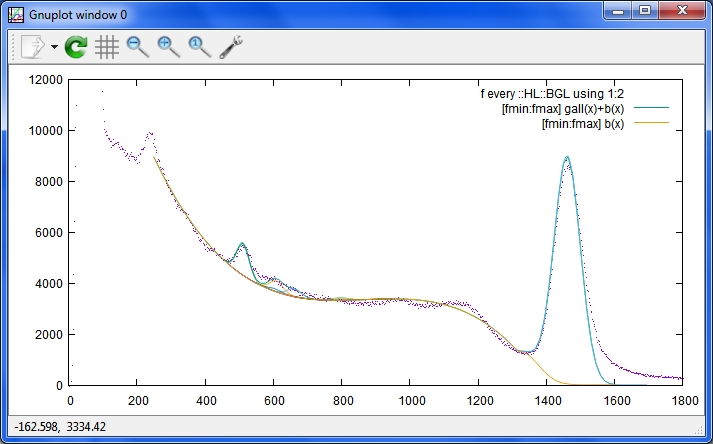
Date: 2015/04/07 08:40(45) --- Name: nkom
これは、CsI2.5インチで、灰化したメープルシロップを測ったスペクトル。
まだ、ぐだぐだですが、別の測定器でも、凄くひどい状態になっないのでやれやれ。
Cs134は、とんでもない誤差になっているし、間違ってピークを割り当てたりしていません。
After 55 iterations the fit converged.
final sum of squares of residuals : 72871.9
rel. change during last iteration : -1.35391e-007
degrees of freedom (FIT_NDF) : 637
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 10.6957
variance of residuals (reduced chisquare) = WSSR/ndf : 114.399
Final set of parameters Asymptotic Standard Error
======================= ==========================
hEc = 38.2662 +/- 8.473 (22.14%)
sEc = 114.769 +/- 13.56 (11.82%)
b0 = 73.7928 +/- 31.57 (42.78%)
b1 = -0.0367191 +/- 0.01956 (53.26%)
cb0 = 0.000199492 +/- 1.65e-005 (8.274%)
cbx = 980.419 +/- 52.85 (5.391%)
cby = 40.7743 +/- 12.42 (30.47%)
hCs137_1 = 80.5121 +/- 2.98 (3.701%)
hBi214_1 = 11.6711 +/- 3.692 (31.64%)
hCs134_1 = -0.363955 +/- 2.559 (703.1%)
hAnn_1 = 20.7616 +/- 3.151 (15.18%)
hK40_1 = 161.552 +/- 3.356 (2.077%)
correlation matrix of the fit parameters:
hEc sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
hEc 1.000
sEc 0.797 1.000
b0 -0.977 -0.848 1.000
b1 0.973 0.839 -0.999 1.000
cb0 0.008 0.006 -0.007 0.007 1.000
cbx 0.900 0.777 -0.925 0.925 -0.345 1.000
cby 0.978 0.857 -0.996 0.993 -0.006 0.919 1.000
hCs137_1 0.013 0.010 -0.013 0.013 0.390 -0.155 -0.003 1.000
hBi214_1 -0.005 -0.004 0.005 -0.005 -0.216 0.053 0.008 -0.239 1.000
hCs134_1 -0.017 -0.013 0.016 -0.016 -0.475 0.170 0.008 -0.368 0.645 1.000
hAnn_1 0.010 0.008 -0.009 0.009 -0.007 -0.052 0.007 0.183 0.039 -0.155 1.000
hK40_1 0.771 0.601 -0.741 0.729 0.010 0.673 0.756 0.017 -0.007 -0.022 0.013 1.000
8.26691228983387e-007, 0.000199491612231112, -18.0161801962026
8.26691228983387e-007, 0.000211046108093378, -18.0161801962026
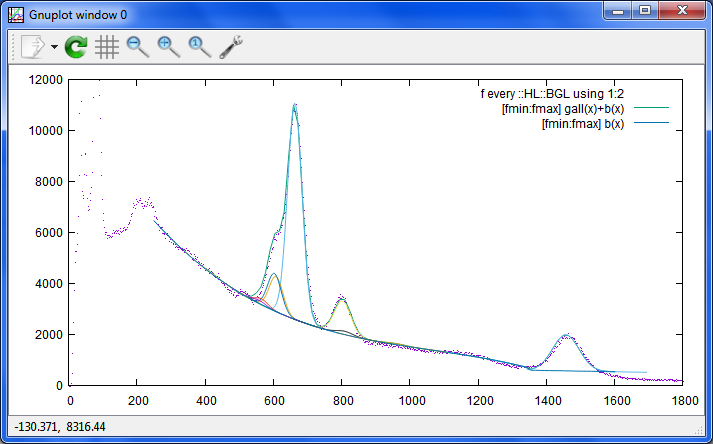
Date: 2015/04/07 08:29(29) --- Name: nkom
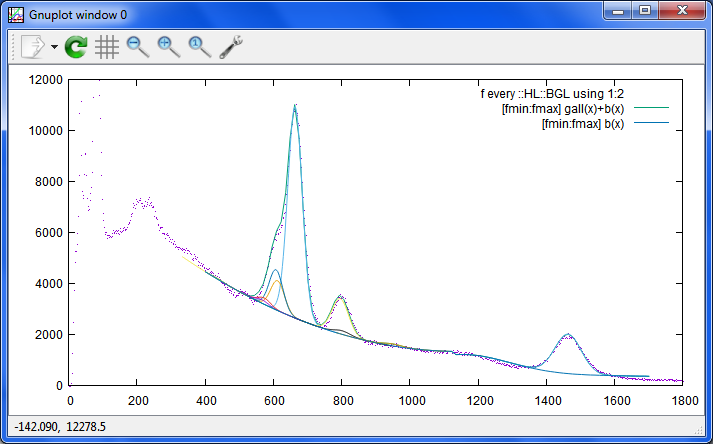
K40が結構あるネスカフェのスペクトルから、日本の汚染土壌20gのスペクトルに変えてみました。
これくらいのK40の変動の範囲であれば、「素人測定レベル」としてなら、まあまあかも。
測定所様、専門家様様のレベルだと、まだ、こんなもんでは、マズイかと思いますが。
あ、これは、自動でエネルギーの再校正をするモードがかかっていたので、
下駄の数値とかが変に動いてます。それでさえも、セシウムの領域とかには、あんまり影響ないみたい。
(というか、セシウムさん達にとことん合わせて、そういう下駄の履かせ方になったわけですし)
Ann(511KeV)は、マイナスになってしまっていますが、絶対値でもって正の側に
縛ってあるので、Gnuplotがピークをマイナスにして、それでもって無理に合わせることは
しないようにしてあります。
After 24 iterations the fit converged.
final sum of squares of residuals : 5.48856e+006
rel. change during last iteration : -3.5543e-006
degrees of freedom (FIT_NDF) : 618
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 94.2399
variance of residuals (reduced chisquare) = WSSR/ndf : 8881.16
Final set of parameters Asymptotic Standard Error
======================= ==========================
hEc = 743.545 +/- 98.18 (13.2%)
sEc = 135.224 +/- 7.335 (5.424%)
b0 = 695.497 +/- 357.9 (51.47%)
b1 = -0.208762 +/- 0.2198 (105.3%)
cb0 = 0.00560828 +/- 0.00016 (2.853%)
cbx = 1129.21 +/- 21.88 (1.938%)
cby = 855.482 +/- 111.6 (13.04%)
ca = 5.1599e-005 +/- 2.167e-007 (0.4199%)
cb = -0.0360902 +/- 0.001956 (5.419%)
cc = 79.2985 +/- 4.358 (5.496%)
hCs137_1 = 8287.63 +/- 33.84 (0.4083%)
hBi214_1 = 1169.81 +/- 37.96 (3.245%)
hCs134_1 = 1378.72 +/- 25.36 (1.84%)
hAnn_1 = -0.538908 +/- 28.36 (5262%)
hK40_1 = 1548.12 +/- 30.02 (1.939%)
correlation matrix of the fit parameters:
hEc sEc b0 b1 cb0 cbx cby ca cb cc hCs137 hBi214 hCs134 hAnn_1 hK40
_1
hEc 1.000
sEc 0.779 1.000
b0 -0.988 -0.811 1.000
b1 0.985 0.802 -1.000 1.000
cb0 0.065 0.037 -0.062 0.060 1.000
cbx 0.848 0.699 -0.863 0.864 -0.437 1.000
cby 0.980 0.819 -0.987 0.984 0.174 0.787 1.000
ca 0.201 0.154 -0.190 0.186 0.321 -0.001 0.226 1.000
cb -0.176 -0.098 0.165 -0.162 -0.330 0.026 -0.199 -0.985 1.000
cc 0.154 0.057 -0.144 0.142 0.332 -0.045 0.176 0.955 -0.992 1.000
hCs137_1 0.131 0.098 -0.124 0.121 0.475 -0.147 0.175 0.610 -0.599 0.578 1.000
hBi214_1 -0.080 -0.047 0.076 -0.074 -0.286 0.065 -0.095 -0.426 0.424 -0.409 -0.453 1.000
hCs134_1 0.087 0.048 -0.082 0.081 0.558 -0.216 0.131 0.414 -0.424 0.424 0.508 -0.667 1.000
hAnn_1 -0.030 -0.018 0.028 -0.028 -0.058 0.052 -0.047 -0.116 0.119 -0.119 -0.211 0.010 -0.196 1.000
hK40_1 0.730 0.443 -0.697 0.689 0.106 0.562 0.710 0.302 -0.292 0.279 0.196 -0.131 0.141 -0.046 1.00
0
4.75998167916391e-005, 0.00560828309411066, -4.00447443141222
5.15989708548341e-005, -0.0360901944992609, 79.2985178361686
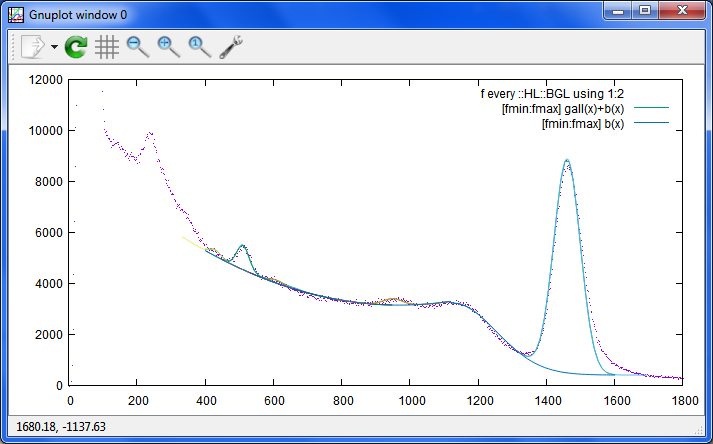
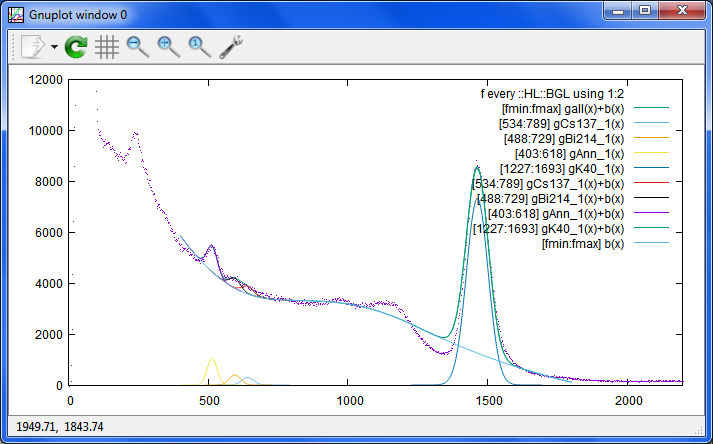
Date: 2015/04/07 08:16(59) --- Name: nkom
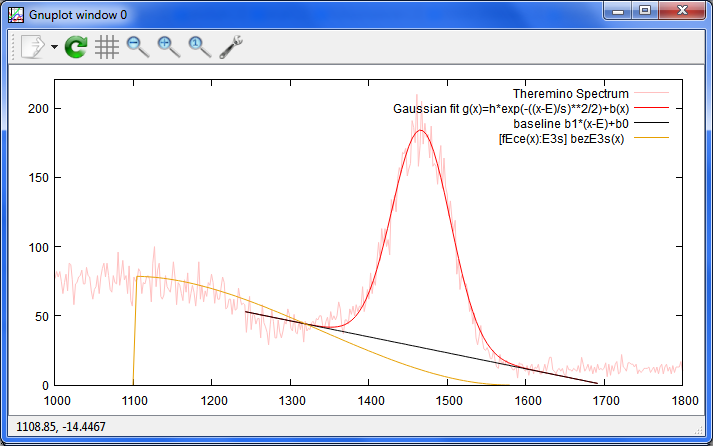
K40のピークの下に直線を追加してみました。
特定のスペクトルに最適化したモデルになっても使い道がありませんし
他のデータでも確認しながらやらないと。
After 11 iterations the fit converged.
final sum of squares of residuals : 8.4544e+006
rel. change during last iteration : -5.73943e-007
degrees of freedom (FIT_NDF) : 618
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 116.963
variance of residuals (reduced chisquare) = WSSR/ndf : 13680.3
Final set of parameters Asymptotic Standard Error
======================= ==========================
hEc = 1732.72 +/- 39.15 (2.259%)
sEc = 66.3017 +/- 1.676 (2.528%)
b0 = 3250.99 +/- 140 (4.305%)
b1 = -1.54455 +/- 0.09008 (5.832%)
cb0 = 0.00693915 +/- 0.0001769 (2.549%)
cbx = 856.901 +/- 7.325 (0.8548%)
cby = 1258.03 +/- 64.27 (5.109%)
hCs137_1 = 23.5697 +/- 32.93 (139.7%)
hBi214_1 = 71.1822 +/- 41.02 (57.62%)
hCs134_1 = 41.6461 +/- 28.21 (67.73%)
hAnn_1 = 928.941 +/- 35.32 (3.802%)
hK40_1 = 7696.8 +/- 27.87 (0.3621%)
correlation matrix of the fit parameters:
hEc sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
hEc 1.000
sEc 0.356 1.000
b0 -0.783 -0.671 1.000
b1 0.768 0.646 -0.997 1.000
cb0 0.004 0.004 -0.004 0.003 1.000
cbx 0.679 0.572 -0.882 0.885 -0.327 1.000
cby 0.780 0.683 -0.978 0.967 -0.140 0.902 1.000
hCs137_1 0.006 0.006 -0.006 0.005 0.374 -0.190 -0.084 1.000
hBi214_1 -0.002 -0.002 0.002 -0.002 -0.219 0.030 0.042 -0.237 1.000
hCs134_1 0.007 0.007 -0.007 0.007 0.465 -0.193 -0.105 0.361 -0.644 1.000
hAnn_1 0.004 0.004 -0.004 0.004 -0.026 -0.134 -0.027 0.180 0.043 0.151 1.000
hK40_1 0.429 0.443 -0.438 0.395 0.009 0.347 0.474 0.013 -0.005 0.017 0.009 1.000
3.51997252906418e-005, 0.00693914963782317, -4.02806250178535
3.51997252906418e-005, 0.00695330680467435, -4.02806250178535
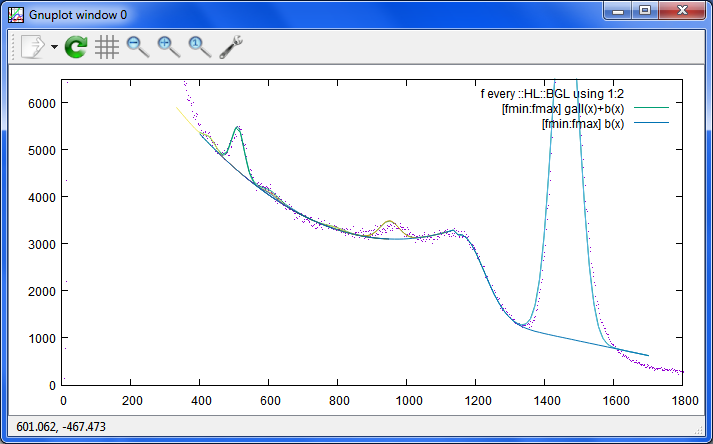
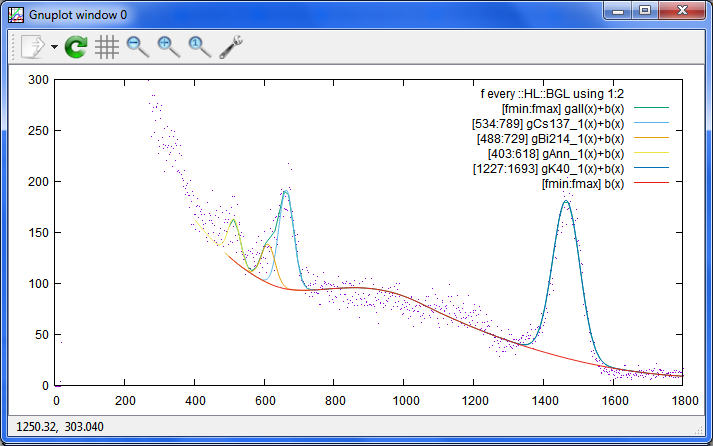
Date: 2015/04/07 07:40(27) --- Name: nkom
わずかに前進。 Sie氏法です。まだバックスキャッターは入れてないし、
式の形も論文のものとは違うので、パラメーターの動き方も今のところ違います。
この例では、無いピークは、ちゃんと誤差が大きく出ていて、
K40や511KeVは、一応少ない誤差になっています。
まあ、K40の右側がズレてますし、問題が山積みなのは変わっていません。
After 7 iterations the fit converged.
final sum of squares of residuals : 2.32356e+007
rel. change during last iteration : -4.13618e-007
degrees of freedom (FIT_NDF) : 572
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 201.548
variance of residuals (reduced chisquare) = WSSR/ndf : 40621.8
Final set of parameters Asymptotic Standard Error
======================= ==========================
hEc = 2820.78 +/- 34.07 (1.208%)
sEc = 126.317 +/- 1.844 (1.46%)
cb0 = 0.00658899 +/- 0.0003292 (4.996%)
cbx = 970.335 +/- 11.77 (1.213%)
cby = 2744.82 +/- 16.5 (0.6012%)
hCs137_1 = 41.9593 +/- 57.32 (136.6%)
hBi214_1 = 114.1 +/- 70.72 (61.98%)
hCs134_1 = 9.05498 +/- 49.08 (542%)
hAnn_1 = 965.109 +/- 60.93 (6.313%)
hK40_1 = 8398.37 +/- 37.19 (0.4428%)
correlation matrix of the fit parameters:
hEc sEc cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
hEc 1.000
sEc -0.592 1.000
cb0 -0.000 0.001 1.000
cbx -0.000 0.000 -0.924 1.000
cby -0.002 0.004 -0.237 0.032 1.000
hCs137_1 0.001 -0.002 0.396 -0.444 -0.255 1.000
hBi214_1 -0.000 0.000 -0.215 0.148 0.200 -0.239 1.000
hCs134_1 0.001 -0.003 0.479 -0.489 -0.380 0.373 -0.641 1.000
hAnn_1 0.001 -0.003 -0.007 -0.164 -0.044 0.185 0.041 0.156 1.000
hK40_1 0.165 -0.334 -0.002 -0.001 -0.013 0.007 -0.001 0.008 0.009 1.000
3.51997252906418e-005, 0.00658898709958903, -4.02806250178535
3.51997252906418e-005, 0.00647176099785374, -4.02806250178535
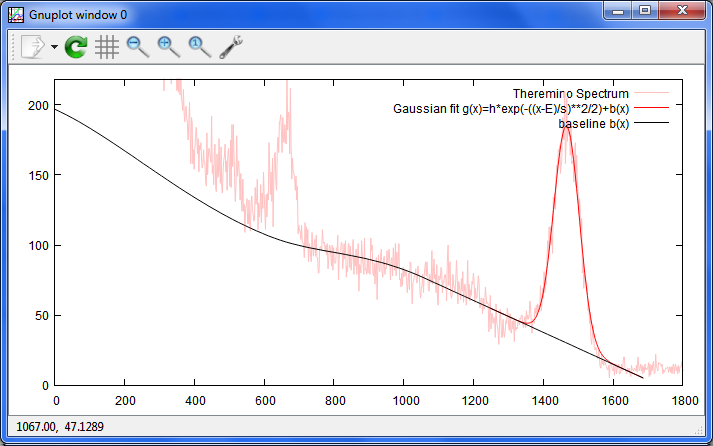
Date: 2015/04/06 11:35(58) --- Name: nkom
とにかく、区分けして、適当な曲線を入れたりすれば良いのと、そのやり方に
少し慣れてきたので、後は、工夫次第。
また、シングルエスケープやダブルエスケープについては、
位置がそんなにズレるものでもないだろう、ということで、
サブピークとして、ウソの放出率で誤魔化せないか?とか思っています。
素人測定の機器だと、それらがはっきり見えるかどうかもありますし、
ウソの放出率がマズイ場合は、そこだけ追加で少し計算をするなり、
縛りを解いて、特定の範囲内でフィットさせるなり、そんなふうにすれば良さそう。
コンプトンエッジとバックスキャッターは、そうは行かないでしょうが。
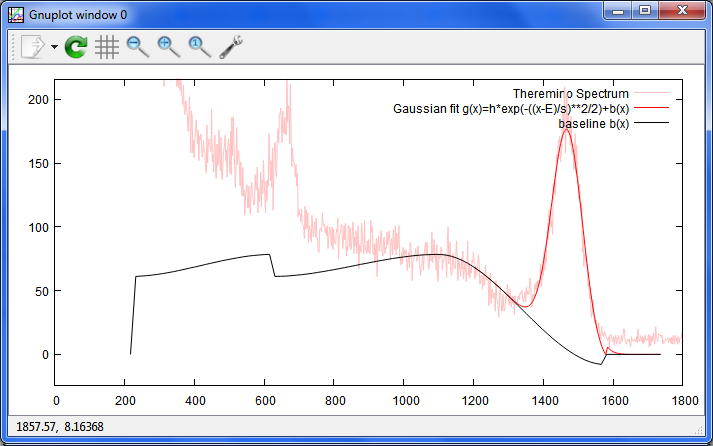
Date: 2015/04/06 11:30(04) --- Name: nkom
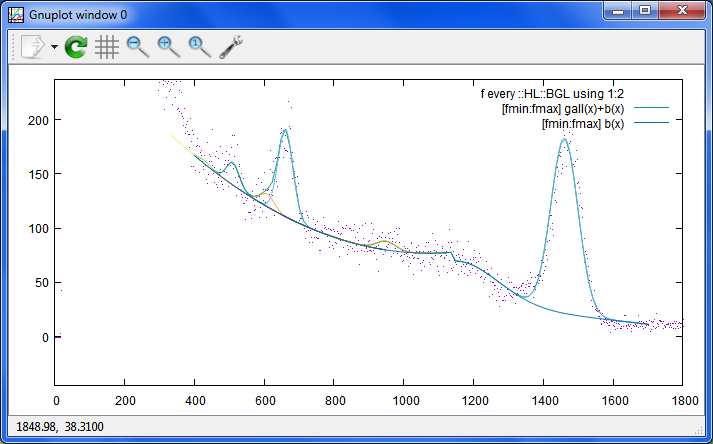
Cs137が検体に20Bqくらい含まれていると、もう、素人測定的には、こんなもんでも
問題ないくらいなのですが、汚染が消滅ピーク以下くらいの微妙なものだと、
もっと頑張らないとなりません。
After 12 iterations the fit converged.
final sum of squares of residuals : 8.02975e+006
rel. change during last iteration : -5.36781e-011
degrees of freedom (FIT_NDF) : 645
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 111.576
variance of residuals (reduced chisquare) = WSSR/ndf : 12449.2
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = 0.0205829 +/- 0.0005993 (2.912%)
bb = -23.882 +/- 0.4547 (1.904%)
bc = 11235.7 +/- 98.26 (0.8746%)
bd = -6.4393e-006 +/- 2.409e-007 (3.741%)
b1 = -0.242706 +/- 0.1673 (68.91%)
b0 = 908.227 +/- 249.8 (27.51%)
ca = -3.46464e-005 +/- 3.997e-006 (11.54%)
cb = 1.15888 +/- 0.007862 (0.6784%)
cc = -70.7211 +/- 3.467 (4.903%)
hCs137_1 = 8477.07 +/- 43 (0.5073%)
hBi214_1 = 1379.88 +/- 39.72 (2.879%)
hCs134_1 = 1286.08 +/- 26.37 (2.05%)
hAnn_1 = -28.086 +/- 33.92 (120.8%)
hK40_1 = 1415.47 +/- 31.04 (2.193%)
Date: 2015/04/06 11:07(20) --- Name: nkom
コンプトンバレーの埋まり方は、少しだけ良くなりましたが、まあ、とにかく、全体的にまだまだです。
これは、三次式で、コンプトン散乱をほぼカバーして、その右は、ガウス曲線の右半分を混ぜたもの。
After 14 iterations the fit converged.
final sum of squares of residuals : 5.70596e+007
rel. change during last iteration : -1.69634e-007
degrees of freedom (FIT_NDF) : 645
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 297.43
variance of residuals (reduced chisquare) = WSSR/ndf : 88464.5
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = 0.0651923 +/- 0.00161 (2.47%)
bb = -56.0894 +/- 1.202 (2.142%)
bc = 19281.5 +/- 258.2 (1.339%)
bd = -2.5031e-005 +/- 6.596e-007 (2.635%)
hEce = 1295.98 +/- 69.48 (5.361%)
Esep = 1324.8 +/- 2.907 (0.2194%)
hCs137_1 = 299.302 +/- 83.23 (27.81%)
hBi214_1 = 423.29 +/- 102.9 (24.31%)
hCs134_1 = 87.6574 +/- 68.22 (77.82%)
hAnn_1 = 1259.4 +/- 89.78 (7.129%)
hK40_1 = 8944.88 +/- 53.54 (0.5986%)
correlation matrix of the fit parameters:
ba bb bc bd hEce Esep hCs137 hBi214 hCs134 hAnn_1 hK40_1
ba 1.000
bb -0.992 1.000
bc 0.964 -0.987 1.000
bd -0.994 0.973 -0.934 1.000
hEce -0.000 0.000 -0.000 0.000 1.000
Esep -0.000 0.000 -0.000 0.000 -0.400 1.000
hCs137_1 0.362 -0.388 0.380 -0.330 -0.000 -0.000 1.000
hBi214_1 0.109 -0.087 0.065 -0.126 -0.000 -0.000 -0.170 1.000
hCs134_1 0.270 -0.310 0.316 -0.226 0.000 0.000 0.322 -0.606 1.000
hAnn_1 0.424 -0.424 0.384 -0.410 -0.000 -0.000 0.257 0.040 0.221 1.000
hK40_1 0.000 -0.000 0.000 -0.000 -0.041 -0.219 0.000 0.000 -0.000 0.000 1.000
3.51997252906418e-005, 1, -4.02806250178535
3.51997252906418e-005, 1, -4.02806250178535
Date: 2015/04/06 08:01(20) --- Name: nkom
こういう文書もあって、Heath氏のデータを使ってよさげな応答関数を作ったらしいのですが、
具体的なデータとか無いし、再現するのは、ちょっと面倒そう。
やるとしたら、PDFの文書のグラフからデータに変換し、この方がやったのと同じ筋道を
やり直すしかないでしょう。
https://www.jstage.jst.go.jp/article/radioisotopes1952/32/3/32_3_101/_pdf
まあ、IAEAの方のやり方でまずやってみて、それでもってあんまり芳しくないようなら
もっと努力するか、検討します。
古い参考書の方は、一応データとか付いているし、文字がかすれたり
PDF化の文字化けみたいのがあるので、式とかを一々確認しながら見ています。
で、ガウス曲線がシグマを使った形ではなく、FWHMを使った形になっているので、
そういう初歩的なことも、一々確かめながらやってます。
f(x)=h*exp(-(x-E)**2/2*sigma**2)
f(x)=h*exp(-4*log(2)/FWHM**2 * (x-E)**2)
統計とかだと、σの形ばっかみたいですが、特定の分野だと
FWHM形式も多いみたい。
で、4ln(2)が2.7726で入っていたりする。
環境放射能.go.jpのNo.29 緊急時のうんたらかんたらでも、この形でやってました。
これ、色々と親切に書かれてますね。
5.2.6.2 放射能濃度の計算〔計算機を用いるが手計算も出来る〕
放射能濃度は次の式にしたがって計算する。
正味計数率 = 試料ピーク面積 / 試料測定時間 − BG ピーク面積 / BG 測定時間
放射能濃度 = (正味計数率 × 減衰補正係数 × 灰分率 × 希釈倍率) /
(ピーク効率 × ガンマ線放出比 × 回収率 × 測定供試量)
灰化も希釈もしてなくて、新鮮な核種を扱っている場合は、分子は「正味計数率」だけ。
あ、このマニュアルに従うのであるなら、「放出率」とかでなく、「放出比」を使うと良いのでしょう。
なんだ、ここにHeath氏の式が解説されていました。62ページ目
http://www.kankyo-hoshano.go.jp/series/lib/No20.pdf
まあ、私が考えていることは、学者さんたちが50年くらい前にやってた様なことを
簡略化したようなものですので、普通は、MCでやるのでしょうが、それをやるには
検出器のモデルだけでなく、遮蔽とか色々とやらないとならないので、
雑多な検出器を利用している素人測定環境では面倒過ぎる。
そこで、出来るだけ簡単な式でモデル化して、後は、ユーザーが自分のスペクトルで
自分の測定環境用のパラメーターを手動か自動で設定すると、
それを元に色々と推測する、という作戦なのです。
MCを使った例。レスポンス関数、というかデータのセットや使い方が載っています。
http://jolissrch-inter.tokai-sc.jaea.go.jp/pdfdata/JAERI-1306.pdf
それにしても、こういうのを見ると、昔は大変だったのだなあ、というのが少し分かります。
今は、GnuplotとかPythonとかOctaveやRとかで、色々なことが凄く簡単に、
早く出来るので、試行錯誤しながらやらないと学ばない私の様な人間にとっては楽になっています。
http://www.kankyo-hoshano.go.jp/series/lib/No6.pdf
Date: 2015/04/05 13:32(02) --- Name: nkom
参考書発見。IAEAの古いドキュメント。文字がかすれちゃってますが、図を見るだけでも
なんとなくやり方が分かるような気がします。
しかも、放物線とガウス曲線二つで済ましているみたい。
Eu152のスペクトルまで再現してしまっている。
http://www.iaea.org/inis/collection/NCLCollectionStore/_Public/10/477/10477396.pdf
Date: 2015/04/05 12:30(12) --- Name: nkom
K40の含有量の多いネスカフェのスペクトルでやってみたら、駄目ですねえ。
明日また考えます。
Date: 2015/04/05 11:25(48) --- Name: nkom
正造 ‏@etosha0824
@dotttotoo こんばんは。植物の異常、最初は異様に生い茂り、それから部分的に弱る木が出始め、妙な伐採がはじまり、今年の春はお気づきのとおりです。最近の変化には私もショックをうけています。@makotokasai さんの記録をご覧になれば、多くのことがわかります。
https://twitter.com/etosha0824/status/583669191959388160
安全安心の「ホルミシス酔い」
Date: 2015/04/05 10:59(23) --- Name: nkom
なかなか難しい。
分解能や結晶の大きさで、コンプトンバレーの埋まり方も変わるし、
コンプトンエッジの最高点のエネルギー位置も変わるし、
そういうものに後々追従できる様な曲線でないといけないのだけど、
基礎知識がないので、どんな関数を使うと良いのか、
一々試さないと、検討がつきません。
そう言えば、NaIのカタログにHeath氏の使った式が載っていた様な。
確かFortranで書いた筈で、どこかにコードが落ちていないのだろうか?
その部分を扱った文書もあったらしいけど、昔の話でPDF化されてないみたいだし、
カタログに載っている式も、PDF化の際に文字化けしているらしきところが
見受けられて、あんまり良く分かりません。
Date: 2015/04/05 10:00(03) --- Name: nkom
バグは直して、効率直線も噛ませたけど、直線ではこんなもん。
Bezier曲線もちょっとそのままだと合わないのかも。
他の曲線も試さないと。
(800keV以降をFitしてみたものです。)
Date: 2015/04/05 09:04(26) --- Name: nkom
バックスキャッターの方まで延長しましたが、まだ効率曲線を噛ませてないし、
あちこちバグってます。
Date: 2015/04/05 08:29(23) --- Name: nkom
Bezier曲線でコンプトン散乱の「再現」もどきをする実験その1。
ピークの右側から、コンプトンエッジまで(と言っても、CEの位置を左にずらしますが)の部分。
先が長そう・・・
Date: 2015/04/04 21:50(52) --- Name: nkom
Eu152とPbXだけにしてみましたが、効率曲線とベースラインをどうにかしないことには、
低い方の高さが合いません。
After 10 iterations the fit converged.
final sum of squares of residuals : 1.30088e+008
rel. change during last iteration : -2.82189e-006
degrees of freedom (FIT_NDF) : 783
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 407.603
variance of residuals (reduced chisquare) = WSSR/ndf : 166140
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = -0.00485685 +/- 0.0005627 (11.59%)
bb = 3.13985 +/- 0.4048 (12.89%)
bc = 381.356 +/- 83.44 (21.88%)
bd = 1.76322e-006 +/- 2.242e-007 (12.71%)
ca = 3.42225e-005 +/- 1.621e-005 (47.37%)
cb = 1.99803 +/- 0.009927 (0.4968%)
cc = -3.05355 +/- 0.4792 (15.69%)
hEu152_1 = 1766.33 +/- 50.41 (2.854%)
hPbx_1 = 1050.37 +/- 170.1 (16.19%)
correlation matrix of the fit parameters:
ba bb bc bd ca cb cc hEu152 hPbx_1
ba 1.000
bb -0.978 1.000
bc 0.841 -0.921 1.000
bd -0.989 0.939 -0.777 1.000
ca 0.100 -0.083 0.060 -0.111 1.000
cb -0.088 0.076 -0.057 0.094 -0.960 1.000
cc 0.093 -0.087 0.075 -0.094 0.637 -0.711 1.000
hEu152_1 -0.459 0.473 -0.547 0.440 -0.072 0.071 -0.066 1.000
hPbx_1 -0.354 0.403 -0.474 0.320 -0.029 0.030 -0.047 0.264 1.000
2.27991135460468e-005, 2.00390539017023, -3.976248747201
3.42225280581207e-005, 1.99802584773861, -3.0535491384057
Date: 2015/04/04 21:38(23) --- Name: nkom
失敗例、その2:
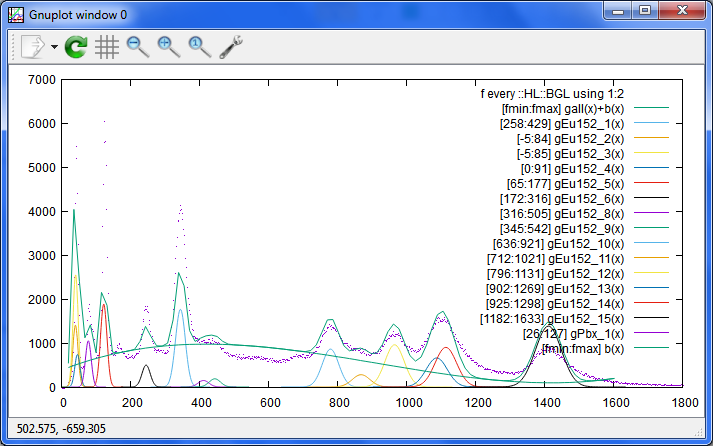
これは、先ほどの設定はそのままで、単にEu152を核種リストに追加したもの。
フィット自体は、Bi214が少しながらマイナスになってしまっていたりするものの、
そんなに酷くはないと思うのですが、凡例が多すぎてスペクトルが見えない、という失敗。
後で、判例を工夫する際に、色と凡例は、それぞれの核種に一つだけにした方が良さそうです。
ただ、さすがEu152というか、校正曲線のフィットは、今までの中で、一番まともかも。
フィットの範囲を広げれば、もっと良くなるかもしれないし、少し期待できそうです。
まあ、そんなことを言っても、表示の工夫をやらないと、何がなんだか分からないかもしれませんが。
After 19 iterations the fit converged.
final sum of squares of residuals : 3.93422e+006
rel. change during last iteration : -7.66736e-006
degrees of freedom (FIT_NDF) : 365
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 103.82
variance of residuals (reduced chisquare) = WSSR/ndf : 10778.7
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = 0.0227853 +/- 0.00221 (9.699%)
bb = -16.8179 +/- 1.642 (9.762%)
bc = 4756.94 +/- 378.3 (7.953%)
bd = -1.02616e-005 +/- 9.483e-007 (9.242%)
ca = -0.000182864 +/- 4.885e-005 (26.71%)
cb = 2.10637 +/- 0.03432 (1.629%)
cc = -9.58473 +/- 4.959 (51.74%)
hCs137_1 = 85.3745 +/- 33.75 (39.54%)
hBi214_1 = -92.6764 +/- 46.52 (50.2%)
hCs134_1 = 37.4595 +/- 39.79 (106.2%)
hAnn_1 = -45.9861 +/- 34.7 (75.46%)
hEu152_1 = 1634.48 +/- 64.99 (3.976%)
correlation matrix of the fit parameters:
ba bb bc bd ca cb cc hCs137 hBi214 hCs134 hAnn_1 hEu152
ba 1.000
bb -0.993 1.000
bc 0.977 -0.995 1.000
bd -0.990 0.967 -0.939 1.000
ca 0.203 -0.271 0.315 -0.104 1.000
cb -0.187 0.253 -0.295 0.088 -0.996 1.000
cc 0.117 -0.180 0.218 -0.023 0.971 -0.987 1.000
hCs137_1 0.460 -0.500 0.517 -0.406 0.267 -0.260 0.219 1.000
hBi214_1 0.038 0.028 -0.080 -0.121 -0.512 0.522 -0.521 -0.265 1.000
hCs134_1 0.344 -0.423 0.474 -0.237 0.668 -0.673 0.645 0.492 -0.742 1.000
hAnn_1 0.495 -0.495 0.475 -0.481 0.178 -0.176 0.155 0.380 0.012 0.285 1.000
hEu152_1 -0.263 0.336 -0.387 0.155 -0.783 0.798 -0.805 -0.258 0.571 -0.715 -0.139 1.000
2.27991135460468e-005, 2.00390539017023, -3.976248747201
-0.000182863881061902, 2.10636875947345, -9.58473446735458
Date: 2015/04/04 21:28(25) --- Name: nkom
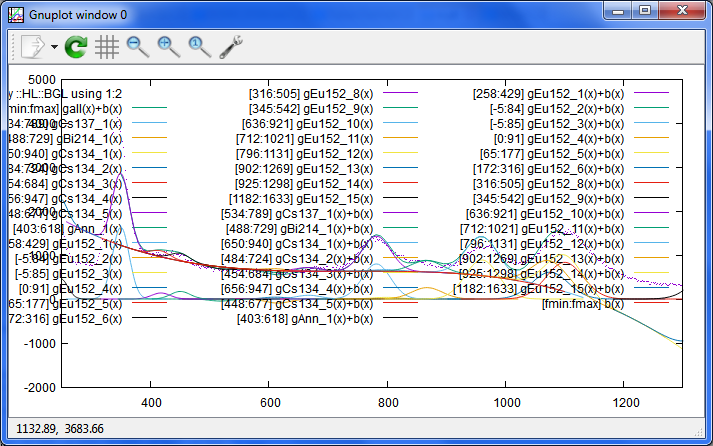
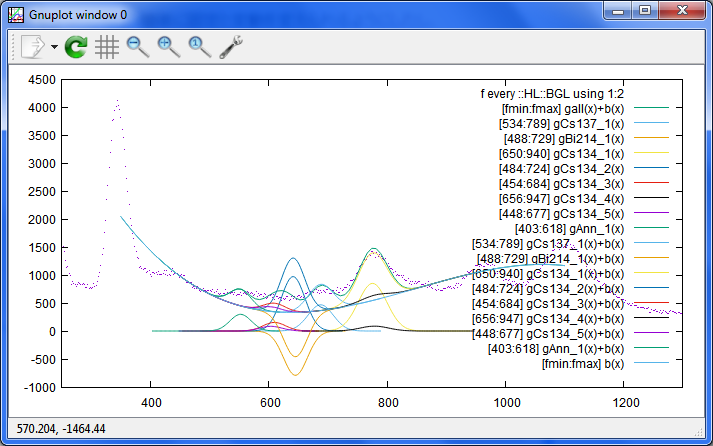
失敗例:
これは、Eu152のスペクトルにしたのだけど、フィットを試みる核種を
Cs134,Cs137,Bi214,Ann(511KeV)のままで、しかもフィットの範囲も変えなかったら、
山を裏返しにしてきてくれたもの。
どういうことかと言うと、Eu152の779keVのピークに、Cs134の795keVを当てはめ、
それと辻褄を合わせるためにBi214の604keVをマイナスにしてしまったのでしょう。
Gnuplot ちょっと頑張りすぎ。 Cs137のピークもあることにしてしまっているし。
After 149 iterations the fit converged.
final sum of squares of residuals : 1.80708e+007
rel. change during last iteration : -8.85992e-006
degrees of freedom (FIT_NDF) : 366
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 222.202
variance of residuals (reduced chisquare) = WSSR/ndf : 49373.8
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = 0.0571846 +/- 0.003929 (6.871%)
bb = -45.5666 +/- 2.832 (6.214%)
bc = 11951.4 +/- 630 (5.271%)
bd = -2.24291e-005 +/- 1.737e-006 (7.743%)
ca = -0.00347999 +/- 0.0001516 (4.357%)
cb = 3.85465 +/- 0.1052 (2.73%)
cc = -206.604 +/- 20.4 (9.875%)
hCs137_1 = 468.945 +/- 74.56 (15.9%)
hBi214_1 = -791.945 +/- 94.17 (11.89%)
hCs134_1 = 851.514 +/- 77.24 (9.071%)
hAnn_1 = 298.198 +/- 77.84 (26.1%)
correlation matrix of the fit parameters:
ba bb bc bd ca cb cc hCs137 hBi214 hCs134 hAnn_1
ba 1.000
bb -0.994 1.000
bc 0.979 -0.995 1.000
bd -0.994 0.976 -0.953 1.000
ca -0.170 0.215 -0.242 0.122 1.000
cb 0.205 -0.251 0.277 -0.156 -0.945 1.000
cc -0.231 0.271 -0.292 0.187 0.770 -0.934 1.000
hCs137_1 0.315 -0.370 0.400 -0.257 -0.409 0.451 -0.441 1.000
hBi214_1 0.063 -0.017 -0.016 -0.107 0.502 -0.478 0.389 -0.448 1.000
hCs134_1 0.263 -0.332 0.372 -0.191 -0.644 0.680 -0.636 0.578 -0.715 1.000
hAnn_1 0.519 -0.546 0.548 -0.482 -0.333 0.339 -0.306 0.409 -0.144 0.436 1.000
2.27991135460468e-005, 2.00390539017023, -3.976248747201
-0.00347999463752709, 3.85465059897709, -206.604196530669
Date: 2015/04/04 21:17(23) --- Name: nkom
強い汚染(と言っても、Cs137の放射能がたった20Bq程度ですが)のスペクトルでは、
ベースラインの三次曲線が上手くいかなかったりしましたが、
微妙な汚染の場合は、これでも結構いい感じ。
それでも、コンプトン丘をやらないと、その部分のカウント数も無駄になるし、もったいない。
Date: 2015/04/04 21:14(08) --- Name: nkom
微妙な汚染の時は、分解能直線のフィットをONにしてしまうと、
Gnuplotが頑張りすぎて変な結果になりがち。
511keVがあるので、校正曲線の方は、ONにしても大丈夫みたい。
逆に言うと、遮蔽の外とかで、ツルペタの場合は、
校正曲線のフィットも切っておかないと、とんでもないエネルギー位置に
もって行かれてしまうかも。
Date: 2015/04/04 21:09(10) --- Name: nkom
同じ粒状炭のスペクトルですが、もっと短時間(1時間)の測定。
まだ、ギザギザで、点で出すとわかりにくいので、線表示。
一応、Bi214はフィットしてますが、Cs137は誤差がかなり大きめ。
After 14 iterations the fit converged.
final sum of squares of residuals : 15466.6
rel. change during last iteration : -1.41224e-008
degrees of freedom (FIT_NDF) : 348
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 6.66665
variance of residuals (reduced chisquare) = WSSR/ndf : 44.4442
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = 0.000570683 +/- 0.0001352 (23.69%)
bb = -0.522922 +/- 0.09546 (18.26%)
bc = 195.319 +/- 20.74 (10.62%)
bd = -2.14868e-007 +/- 6.052e-008 (28.16%)
ca = -0.000239836 +/- 0.001144 (477%)
cb = 2.45074 +/- 0.6255 (25.52%)
cc = -88.4256 +/- 89.5 (101.2%)
hCs137_1 = 2.45014 +/- 2.118 (86.43%)
hBi214_1 = 7.4265 +/- 2.822 (38%)
hCs134_1 = 0.377879 +/- 1.714 (453.7%)
hAnn_1 = 14.4242 +/- 3.125 (21.67%)
correlation matrix of the fit parameters:
ba bb bc bd ca cb cc hCs137 hBi214 hCs134 hAnn_1
ba 1.000
bb -0.996 1.000
bc 0.985 -0.996 1.000
bd -0.996 0.985 -0.968 1.000
ca -0.514 0.523 -0.514 0.497 1.000
cb 0.482 -0.494 0.487 -0.463 -0.971 1.000
cc -0.430 0.444 -0.439 0.411 0.895 -0.976 1.000
hCs137_1 0.340 -0.376 0.394 -0.301 -0.327 0.288 -0.240 1.000
hBi214_1 0.547 -0.540 0.523 -0.546 -0.475 0.459 -0.422 0.119 1.000
hCs134_1 -0.088 0.043 -0.011 0.130 -0.046 0.112 -0.162 0.279 -0.481 1.000
hAnn_1 0.616 -0.628 0.617 -0.596 -0.713 0.721 -0.693 0.393 0.454 0.142 1.000
9.60117535958298e-006, 2.00390539017023, -4.08646109812452
-0.000239836129782265, 2.45074335983124, -88.425581182625
Date: 2015/04/04 20:57(27) --- Name: nkom
もっと微妙な汚染の粒状炭
一応Cs137とBi214のピークをフィットしてます。両方とも標準誤差が30%近いですが。Cs134は、103%
After 13 iterations the fit converged.
final sum of squares of residuals : 87568
rel. change during last iteration : -9.71492e-007
degrees of freedom (FIT_NDF) : 348
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 15.8629
variance of residuals (reduced chisquare) = WSSR/ndf : 251.632
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = 0.00245137 +/- 0.0003521 (14.36%)
bb = -2.28972 +/- 0.2518 (11%)
bc = 902.968 +/- 54.86 (6.075%)
bd = -9.19402e-007 +/- 1.552e-007 (16.88%)
ca = -0.000479757 +/- 0.0007203 (150.1%)
cb = 2.0732 +/- 0.4345 (20.96%)
cc = 18.0331 +/- 65.98 (365.9%)
hCs137_1 = 21.4334 +/- 5.803 (27.07%)
hBi214_1 = 22.7981 +/- 6.484 (28.44%)
hCs134_1 = 4.33411 +/- 4.462 (103%)
hAnn_1 = 67.0384 +/- 8.011 (11.95%)
correlation matrix of the fit parameters:
ba bb bc bd ca cb cc hCs137 hBi214 hCs134 hAnn_1
ba 1.000
bb -0.997 1.000
bc 0.989 -0.997 1.000
bd -0.997 0.988 -0.975 1.000
ca -0.533 0.539 -0.530 0.520 1.000
cb 0.527 -0.536 0.529 -0.511 -0.978 1.000
cc -0.508 0.518 -0.512 0.491 0.934 -0.988 1.000
hCs137_1 0.492 -0.510 0.515 -0.469 -0.392 0.322 -0.264 1.000
hBi214_1 0.268 -0.255 0.241 -0.276 -0.189 0.256 -0.297 -0.211 1.000
hCs134_1 0.379 -0.416 0.434 -0.339 -0.347 0.383 -0.399 0.413 -0.353 1.000
hAnn_1 0.684 -0.691 0.678 -0.668 -0.727 0.740 -0.730 0.447 0.240 0.452 1.000
9.60117535958298e-006, 2.00390539017023, -4.08646109812452
-0.000479756645128492, 2.07319604109217, 18.0331018901011
Date: 2015/04/04 20:47(24) --- Name: nkom
灰化したメープルシロップのスペクトルでテスト
目で見れば、ピークがあるのは分かりますが、Cs137のピークで(29.43%)の標準誤差。
After 12 iterations the fit converged.
final sum of squares of residuals : 46522.2
rel. change during last iteration : -2.20102e-006
degrees of freedom (FIT_NDF) : 366
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 11.2743
variance of residuals (reduced chisquare) = WSSR/ndf : 127.11
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = 0.00207463 +/- 0.000252 (12.15%)
bb = -1.80949 +/- 0.1795 (9.919%)
bc = 623.388 +/- 38.86 (6.234%)
bd = -8.06477e-007 +/- 1.115e-007 (13.83%)
ca = 1.30929e-005 +/- 0.002194 (1.676e+004%)
cb = 2.03119 +/- 1.339 (65.91%)
cc = -27.7219 +/- 200.7 (723.9%)
fa = 0.0569113 +/- 0.06828 (120%)
fb = 17.1381 +/- 34.55 (201.6%)
hCs137_1 = 87.6098 +/- 25.78 (29.43%)
hBi214_1 = 17.6281 +/- 9.108 (51.67%)
hCs134_1 = 3.80811 +/- 3.372 (88.56%)
hAnn_1 = 28.8044 +/- 8.313 (28.86%)
correlation matrix of the fit parameters:
ba bb bc bd ca cb cc fa fb hCs137 hBi214 hCs134 hAnn_1
ba 1.000
bb -0.997 1.000
bc 0.987 -0.997 1.000
bd -0.997 0.987 -0.973 1.000
ca -0.162 0.166 -0.167 0.156 1.000
cb 0.163 -0.167 0.168 -0.157 -1.000 1.000
cc -0.163 0.167 -0.168 0.157 0.998 -0.999 1.000
fa -0.419 0.412 -0.396 0.419 0.703 -0.705 0.705 1.000
fb 0.485 -0.476 0.456 -0.486 -0.415 0.417 -0.418 -0.936 1.000
hCs137_1 0.206 -0.213 0.215 -0.198 -0.990 0.990 -0.990 -0.724 0.445 1.000
hBi214_1 0.251 -0.239 0.227 -0.260 -0.819 0.821 -0.821 -0.701 0.476 0.817 1.000
hCs134_1 0.286 -0.327 0.350 -0.242 -0.501 0.502 -0.502 -0.382 0.271 0.535 0.147 1.000
hAnn_1 0.324 -0.331 0.329 -0.312 -0.893 0.894 -0.894 -0.578 0.313 0.901 0.744 0.549 1.000
8.26691228983387e-007, 2.00390539017023, -18.0161801962026
1.30929387598989e-005, 2.03118523824745, -27.7218893614872
Date: 2015/04/04 19:38(47) --- Name: nkom
春分も過ぎて、イースターだっていうのに、雪も降るし、今夜はマイナス15まで下がるそうです。
地球温暖化が詐欺だという話は良く有りますが、私はここの冬が2週間くらい短くなる程度の
地球温暖化が本当だったら嬉しいです。
でも冬は、しっかりと寒くてフワフワの雪が降るくらい寒くなって欲しいです。
冬に雨が降るのは、許せません。
冬にマイナス5度くらいまで気温が高まると、暑くて困ります。
ここの冬は気持ちが良いのですが、それでもやっぱり少し長過ぎ。
夏の期間は、丁度良いし、秋も悪くないので、後は、春にもう少し頑張って欲しいです。
Date: 2015/04/04 15:10(13) --- Name: nkom
しかし、こういうことをしていると、テレミノMCAの自動定期保存機能で、
時間とかをファイル名に使うのではなく、3桁とか4桁の連番で
ファイルを保存できるようにした方が、何かと便利かもしれません。
また、色々とテストをしているうちに、3600秒で定期保存する指定をすると、
実は3599秒で保存する場合がほとんどで、秒数のカウントを一つ
間違っていたらしいことが分かったので、それも直さないと。
Date: 2015/04/04 15:03(47) --- Name: nkom
コンプトン丘をやったら、グラフのTitleと言いますか、凡例に何を出すか、とかも、
ちょっと考えます。
核種と、エネルギーと、高さ(cps)、FWHM(パーセントとエネルギー)とか。
それと、校正曲線の式や、分解能直線の式も出した方が分かりやすいし。
で、効率曲線も、やっぱりちゃんとやらないと低い方は合わないし、
それもグラフ上に表示した方が良いでしょう。
そして、そういう曲線の式に、使う関数のバリエーションを増やして、
それを簡単に選択出来る様にして、
ピークのフィットも単純なガウス関数だけじゃなくて、
左右にスカートを履かせたり、CZTのスペクトルでも実験できる様な関数にしたり、
もっと一般化すると、使いやすくなりそう。
こういう事が全部、「Gnuplotだけ」で出来てしまうというのは、予想外でした。
Date: 2015/04/04 14:55(16) --- Name: nkom
Gnuplotでピークフィットする方は、校正曲線のフィットに続いて、分解能直線もフィットさせ、
ついでにベースラインを三次曲線にして、左右を長めにしてみましたが、
校正曲線と分解能曲線は、効果がうかがえますが、ベースラインは、まだまだです。
それに、数値的には、校正曲線の数字も変ですし、全体的に誤差も大きくなってるし・・・
まあ、ベースラインのパラメーターは、出鱈目な初期値を入れたので、そのせいもあるかも。
ともかく、変動させた方が良さそうなところは、簡単に固定と変動を変えられるようにしたし、
次は、コンプトン丘をBezierで試してみようと思います。
After 136 iterations the fit converged.
final sum of squares of residuals : 2.75088e+006
rel. change during last iteration : -5.58965e-006
degrees of freedom (FIT_NDF) : 355
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 88.0281
variance of residuals (reduced chisquare) = WSSR/ndf : 7748.95
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = 0.0288659 +/- 0.001859 (6.439%)
bb = -30.3002 +/- 1.327 (4.379%)
bc = 12714.8 +/- 289.8 (2.279%)
bd = -9.80422e-006 +/- 8.244e-007 (8.408%)
ca = -0.000965573 +/- 0.0001224 (12.67%)
cb = 2.73263 +/- 0.08593 (3.145%)
cc = -132.472 +/- 15.07 (11.38%)
fa = 0.0560971 +/- 0.007048 (12.56%)
fb = 15.878 +/- 4.696 (29.58%)
hCs137_1 = 8352.51 +/- 248.2 (2.972%)
hBi214_1 = 1130.83 +/- 56.88 (5.03%)
hCs134_1 = 1393.79 +/- 49.96 (3.584%)
hAnn_1 = 69.6798 +/- 31.97 (45.89%)
correlation matrix of the fit parameters:
ba bb bc bd ca cb cc fa fb hCs137 hBi214 hCs134 hAnn_1
ba 1.000
bb -0.995 1.000
bc 0.983 -0.996 1.000
bd -0.995 0.981 -0.962 1.000
ca -0.369 0.392 -0.400 0.341 1.000
cb 0.369 -0.393 0.401 -0.340 -0.997 1.000
cc -0.366 0.391 -0.400 0.337 0.990 -0.998 1.000
fa -0.302 0.266 -0.235 0.331 0.126 -0.105 0.084 1.000
fb 0.197 -0.156 0.124 -0.234 0.179 -0.199 0.219 -0.952 1.000
hCs137_1 0.386 -0.413 0.423 -0.354 -0.989 0.993 -0.992 -0.077 -0.226 1.000
hBi214_1 0.308 -0.312 0.308 -0.300 -0.732 0.736 -0.736 0.074 -0.311 0.737 1.000
hCs134_1 0.416 -0.456 0.474 -0.370 -0.891 0.889 -0.883 -0.157 -0.109 0.896 0.477 1.000
hAnn_1 0.563 -0.578 0.569 -0.538 -0.378 0.381 -0.382 -0.045 -0.059 0.403 0.285 0.454 1.000
4.75998167916391e-005, 2.00390539017023, -4.00447443141222
-0.000965573495867557, 2.73263295005192, -132.472012848074