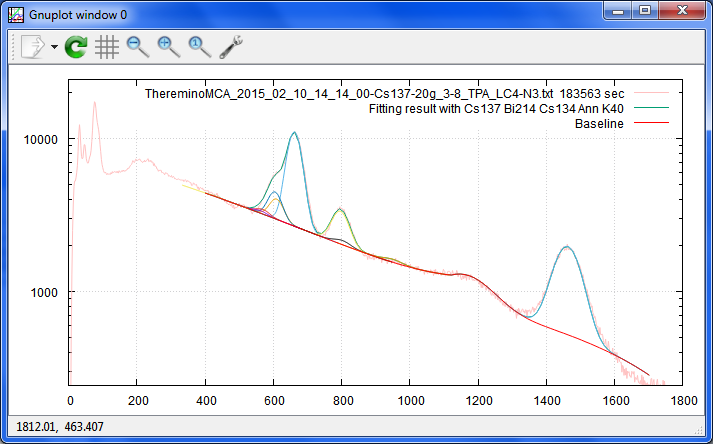
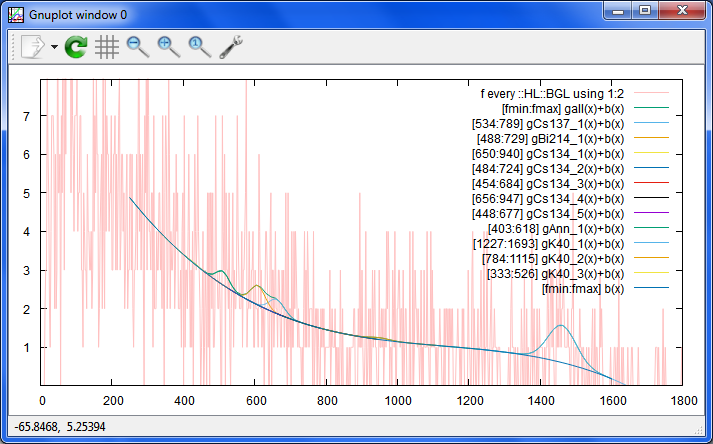
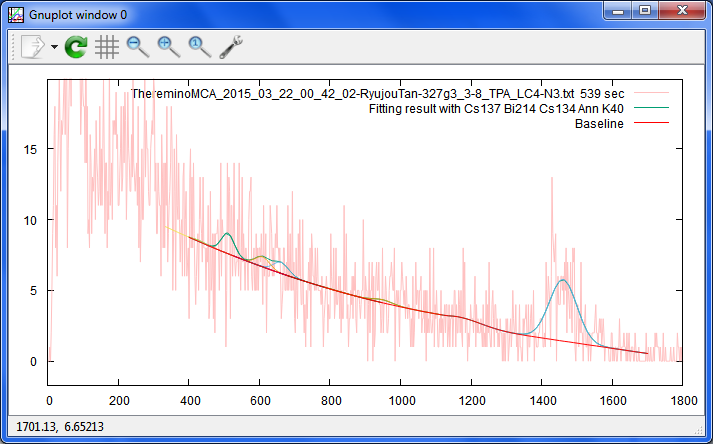
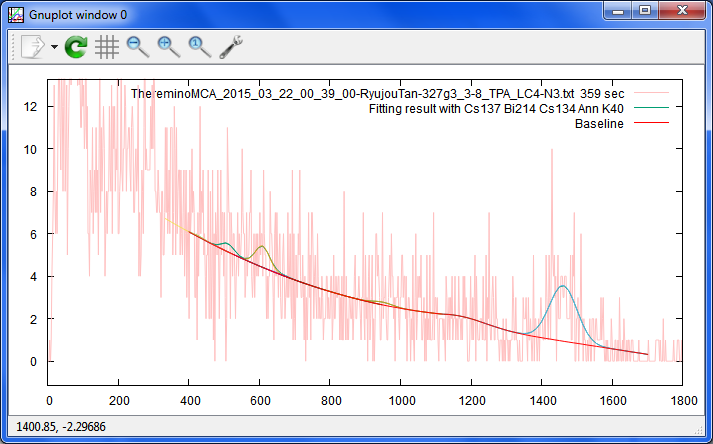
Date: 2015/04/12 01:52(50) --- Name: nkom
K40を追加してみたけど、山がきちんと持ち上がってくれない。どうしてだろう?
ベースラインは、折れ線の右側を放物線にしてみましたが、放物線って、あんまり合わない。
左側でもう少しきつく曲がって、右でもう少しゆるーくなって欲しいので、
平方根の下側でも使えば良いのかも。
学者様に言わせると、こういう「モデル」に基づかないやり方は外道なのでしょうが、
お洋服の世界、というか、オートクチュールでも、型紙をモデル化や理屈で作るのではなく、
人形の上に紙を当てて、そうして形を切り出す、という方法もあったりしますし、
造船や飛行機の世界でも、理屈とは(ほぼ)無縁のテキトーな曲線をでっち上げるのは、
よくあることでしたし、素人測定のベースラインを、一生懸命色々積分したりして
頑張っても、マリネリの形もきっちりとしてなかったり、遮蔽の形も様々だったりするので、
「現場主義」というか「工学的」というか「辻褄合わせのやっつけ仕事」というか
「リバースエンジニアリング」みたいな感じでないと、私にはやっていけません。
有能な方が、デジカメで遮蔽や測定器やマリネリの写真を撮ると、
それを3Dモデル化して、MCでちゃっちゃと応答関数を練り上げて、
それでもってフィットして核種判定から定量的な方まで持っていくようなものを
作ってくれると嬉しいですが、まあ、あんまり期待しないで待っています。
Date: 2015/04/12 01:12(35) --- Name: nkom
どうも、Identify.exeのRa226の核種データが変じゃないのか?ということで、
NaIやGeのカタログと照らし合わせて幾つか削除したら、ベースラインを430keVで
曲がった折れ線にして、こんな感じ。
Identify.exeの核種データが娘核種のピークとかについては、信用できないみたい。
つまり、Ra226のデータでもって、Bi214やPb214が平衡状態にあると仮定して、
放出率を正規化してあるのかと思ったら、そうではなくて、自分で計算しないとならないみたい・・・
Date: 2015/04/12 00:15(10) --- Name: nkom
特性調査で割り出した効率曲線は、一応t使えそう。
Date: 2015/04/11 22:31(23) --- Name: nkom
要は、隣のピークとの距離と、その高さと、分解能でもって、
どれくらい影響が出るのか決まるのですが、
そんなの前もってわかんないし、
左右のピークの下調べフィットをしてから、と思っても、
目当てのピークがそれに絡んでくるわけなので、
一挙にやった方が良くて、
その場合、そのまた左右に近いピークがあったら、
それもやらないと上手くいかないし、
あんまり距離を広げると、分解能やら効率やらの変化が
絡んできたりするし、
欲張ると上手くいかないけど、欲張らないと上手くいかない、という感じです。
まあ、しょうがないので、ウラン原石の場合は、このピーク群をまとめて扱い、
Eu152のこれらをまとめて扱う、という風にするしかないのかも。
(測定器の特性を調べるための自動調査をする場合は、の話ですが。)
単一ピークを調べるには、全体の様子が分からないと駄目で、
全体の様子を分かるには、単一ピークが知りたい、ということで、
困ったものです。
Date: 2015/04/11 22:21(25) --- Name: nkom
任意の単一ピークを調べる際に、自動的に左右のありそうなピークを調べて、
それも一緒にフィットできないか?という実験。
核種データのリストから、左右6シグマくらいで検索し、当てはまるピークをリストアップして、
それを絡めてフィットしよう、と、そう思ったのですが、これも、色々と難しいです。
Date: 2015/04/11 19:41(55) --- Name: nkom
自由自在@dnanoca
そう?騒いだ方が良くね?福島第一原発事故後に学んだことは「線量に敏感になっとけ」だわ。RT
http://twitter.com/dnanoca/status/586855628452204544
誰も騒がないと、分からないで終わることもあるし、見張っていて騒いでくれる人も重要。
だけど、そういう人たちの「結論」や「考え方」は、問題が多かったりする。
毎日線量を見張るのは、結構疲れるので、そういうことに熱心になって、
しかもそれを持続するのは、大変。
ちょっとくらい考え方に問題でもないと、続かなかったりするのかも。
そもそも、線量を見張っていても、大したことは分からないのが分かると、
そんなに「やる気」は、沸きません。
スペクトルを見張っていても、そんなに分からないし、どちらにしろ、
自分のモニタリングで、何か確実なことが分かったりしたら、
初期被爆をしているわけです。
なので、被爆したくなかったら、遠く遠くに住むしかないかも。
そして、それに加えて、近くの人がモニタリングして、
それを報告している必要もあります。
要は、全世界モニタリングネットワークがないと、
初期被爆は避けられません。
CTBTとかがリアルタイムでスペクトルや解析結果を
報告すると良いのですが、そういう期待は出来ないので、
自分たちで勝手にやるのが一番良いのですが、
まあ、関心がある人がそもそも少ないし、
関心があってもお金や技術のある人も少ないし、
現在ほぼリアルタイムでスペクトルが見えるのは、
Pow2P様のところと、私のところくらいかも。
(バークレーは、機器の保守か修理でダウン中)
Pow2P様のところは3ccなので、見えるのに時間がかかります。
私のところは2.5インチだけど、素人機器で、CsIなので、
低い方がちょっと分かりにくかったりします。温度補償もないです。
音楽マニアや各種の熱心な趣味の人たちが、多大な時間やお金を
様々なことに費やしていますが、たった数万円の初期投資で出来る
スペクトルモニタリングが少ない上、その公開をする人は、
世界中でも2,3人しかいないのが現状。
そういう状況では、初期被爆を避けるのは、無理。
なので、防御も無理。
それが嫌なら、3ccでも1インチでもよいので、
各自でスペクトルモニタリングをして公開し、
そういう人が世界中で百人とか千人も居ると、
少し様子が分かるようになるでしょう。
それでも、あまり代わり映えのしないデータを
何年も何十年も見ることになるのですが、
変わったデータをしばしば見るよりも、
いつも何も見えない方が平和なのです。
Date: 2015/04/11 14:18(17) --- Name: nkom
分解能の線があんまり芳しくないですが、エネルギー校正や、効率曲線は
綺麗にモデル化できそうなので、やれやれ。
これで、コンプトン散乱や、他の工夫に戻って、色々とやっつける予定です。
Date: 2015/04/11 14:15(23) --- Name: nkom
こういうので、何をやっていたかというと、ウラン原石のスペクトルを使って、
測定器の特性データを調べていたわけです。
http://pico.dreamhosters.com/PeakFitWithGnuplotPart4.html
この情報とか、やり方を元に、測定器の特性を(できるだけ)自動で調べて、
それを測定データの解析に役立てる様な、そんな仕組みをでっち上げるのが目的です。
Date: 2015/04/11 10:16(45) --- Name: nkom
テレミノ形式以外のスペクトルのデータでも、基本的にやることは同じなのですが、
エネルギーが含まれているかどうか?などで、あちこち変更が必要になります。
特に、準備用のスクリプトは、ほとんどテレミノMCAに特化した部分なので、
そこを変更する必要がありますが、スペクトルデータの読み出しとか
調査に使う小技は同じなので、流用できるでしょう。
SPE形式の場合だと、チャンネルデータにエネルギーが含まれていないので、
エネルギーは後回しにして、チャンネル番号でもって調査したり、フィットして、
後からエネルギーに変換する方が良さそう。
Date: 2015/04/11 10:13(11) --- Name: nkom
色々やっていて、その際に「任意の単一ピーク用フィット」のスクリプトも
改造したので、ページの内容とスクリプトを更新しました。
基本的なことは、変わっていませんが、高さがカウント数だったのを、
測定秒数で割ってレートで扱う様にしたし、マイナスにならない様に
絶対値にしたり、表示に差分を追加したり、といった点です。
http://pico.dreamhosters.com/PeakFitWithGnuplotPart2.html
スクリプトは、この二つ。
これが準備用
http://pico.dreamhosters.com/raddata/ft0.plt
こっちが実際のフィット
http://pico.dreamhosters.com/raddata/ft1.plt
f='ThereminoMCA_2015-04-01.txt'
という感じでfにファイル名をセットして、
load 'ft0.plt'
とやって準備完了。
後は、調べたいピークのエネルギーをEに入れて、ft1を走らせるだけ。
ft1を走らせるコマンドは、マクロに登録済みなので、@ft1で大丈夫。
E=609
@ft1
そうすると、まずは、拡大図でプロットされます。
全体像を見たい場合は、@pla とやるだけ。
あるいは、Shift−xやShift−yでズームアウトしても良いですが。
これで、色々なピークの情報が分かりますが、やってみると、nの値で結構変わるので、
それをどう(自動的に)設定するか、というのが、(私にとっては)問題です。
Date: 2015/04/09 08:48(54) --- Name: nkom
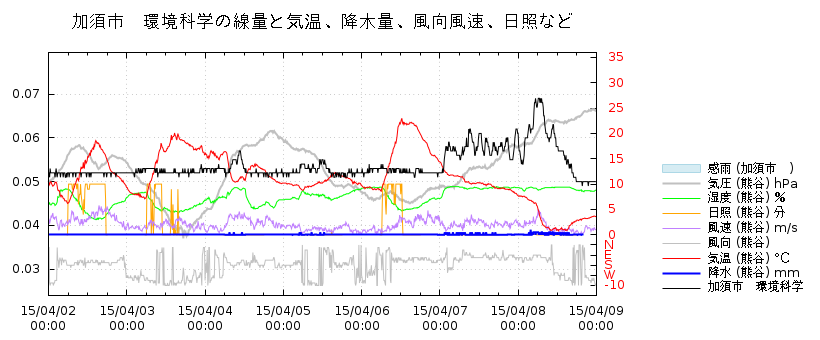
大田ってこれのことなのかな?
特に異常には、見えませんが。
こことか、雨で長い間少し上がったままだったけど、ようやく下がった。
風も弱く、安定して雨がしとしと降り続いたのかも。
他の地点も、私が見ているところで、特に異常だと思うところは、ありませんでした。
変な「リアルタイム線量計」を沢山増設するなら、スペクトルが取れるまともな機械を
少なめに増設した方が、よっぽど確かなことが分かるかと思います。
Date: 2015/04/09 08:28(57) --- Name: nkom
なむるる ‏@namururu
ふおおお!!やっぱり不具合っているモニタリングポスト JBジャパンブランド製やーーーwww
https://twitter.com/namururu/status/585795601620566017/photo/1
ええええええええ?????!!!!!
と、たまに私も叫んでみたりする。
JBジャパン ブランド、って、「ニッポン財団」と同じで、
ジャパンって付いているけど日本と関係ない国の製品で、
ロクでもない「ベクレルモニター」とか売りまくって、
自治体で間違って買ってしまったところがあって、
変なことになっていた会社じゃなかったでしたっけ?
そんなところから、MP(というか、リアルタイム線量計システム)を
買ってしまったのは、どこの役所なんでしょうか?
DoseRae2を入れた機械を採用してしまうのと同じくらいマズイのでは?
だから、やたらと増殖した新しいポイントは、「使えない機械」が多かったのか、
と、納得できそう。
(本当にそうかどうかは、未確認ですし、Gnuplotで忙しいし調べる気も起きませんが)
Date: 2015/04/09 07:30(39) --- Name: nkom
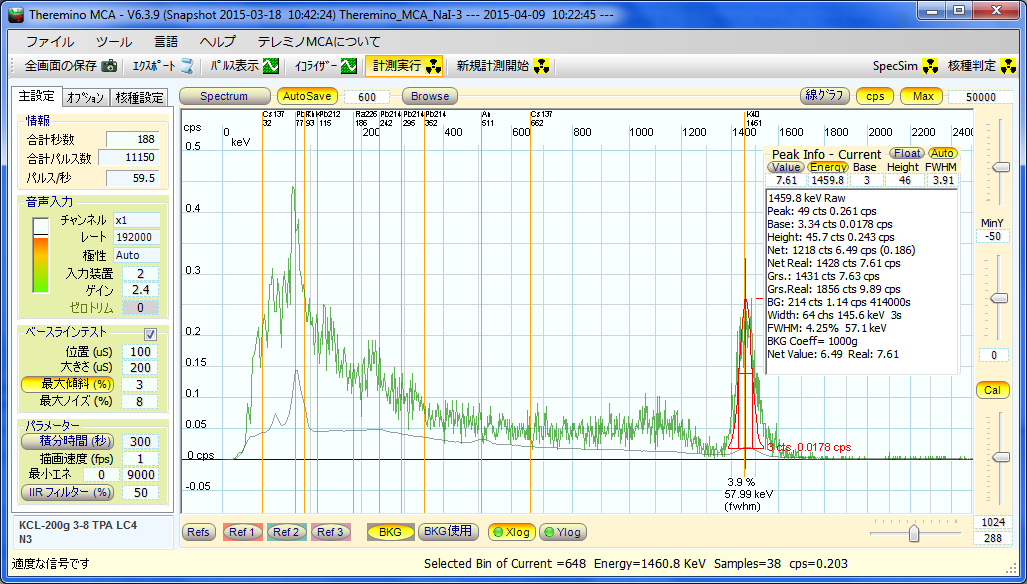
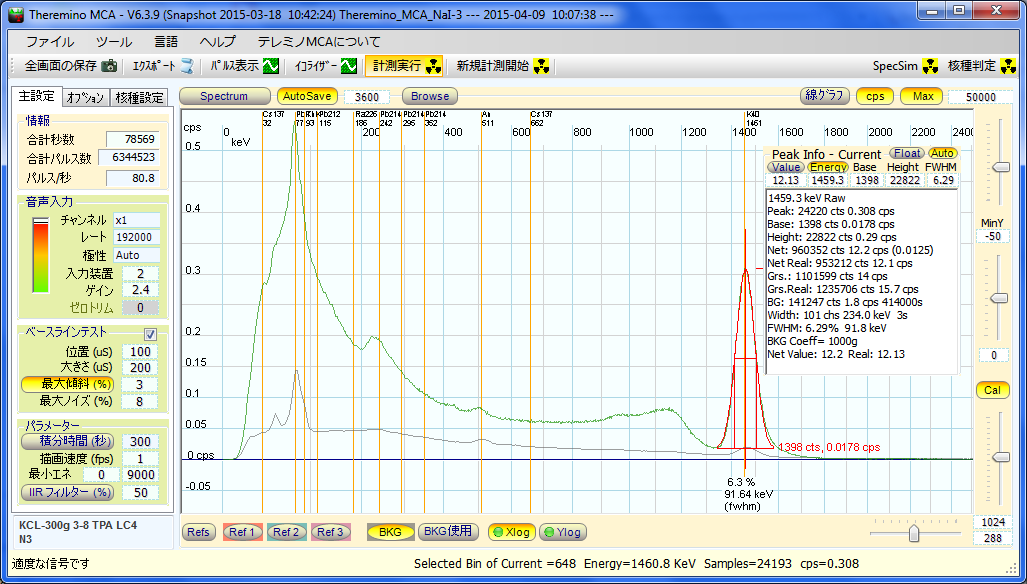
KCL(NoSalt) 200g 188秒。
300gで全体で80.8cpsあって、BGが大体10cpsなので、80.8−10=70.8cpsがKCLの分。
200gだと 70.8 x 200g/300g + 10=57.2cps という予想ですが、ちょっと高め。
レートは、計算からの予想より、4%くらい大きいです。
マリネリの縦割り分割法でやっているのですが、少し効率が高くなる詰め方をしてしまったのかも。
Date: 2015/04/09 07:11(44) --- Name: nkom
KCL(NoSalt)300gのスペクトルは、まあ、こんな感じで十分だろうと思うので、
KCLの量を減らして、次のデータを取ります。
Date: 2015/04/09 06:56(14) --- Name: nkom
ウラン原石のスペクトルで試してみると、他の色々な課題が分かります。
まあ、現在やっているのは、まず、K40のピークだけフィットし、その高さで、
コンプトンエッジを決定。そしたら、コンプトン散乱の丘を三次式と消滅ピーク(511keV)でフィット。
で、最後に、そのコンプトン丘を使って、他の核種のフィット、という形です。
これは、K40のピークから(というか、最終的には任意のエネルギーのピークから)
そのコンプトン散乱のパターンを再現する為のデータを集めるのが目的で、
もし、コンプトン丘の再現が出来る様になったら、その関数は、ピークのガウス曲線と一緒に、
一発でフィットさせるわけです。
なので、その場合には、K40が沢山あろうが、なかろうが、関係なくなるのですが、
今の段階では、K40があるのを前提としているので、ウラン原石とかだと、
変なところにコンプトン散乱の線を引いてしまいます。
After 12 iterations the fit converged.
final sum of squares of residuals : 103.241
rel. change during last iteration : -7.078e-006
degrees of freedom (FIT_NDF) : 924
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.334264
variance of residuals (reduced chisquare) = WSSR/ndf : 0.111732
Final set of parameters Asymptotic Standard Error
======================= ==========================
sK40_4 = 1296.69 +/- 4.976e+005 (3.838e+004%)
eK40_1 = 1420.96 +/- 8.856 (0.6232%)
hCs137_1 = 0.138827 +/- 0.07666 (55.22%)
hCs134_1 = 0.000387549 +/- 0.05431 (1.401e+004%)
hBi214_1 = 0.595195 +/- 0.0805 (13.52%)
hAnn_1 = 2.61891e-005 +/- 0.08231 (3.143e+005%)
hK40_1 = 0.348682 +/- 0.05511 (15.81%)
hPb214_1 = 2.06578 +/- 0.08413 (4.073%)
hPbx_1 = 2.23858 +/- 0.1289 (5.757%)
correlation matrix of the fit parameters:
sK40_4 eK40_1 hCs137 hCs134 hBi214 hAnn_1 hK40_1 hPb214 hPbx_1
sK40_4 1.000
eK40_1 0.006 1.000
hCs137_1 0.000 0.005 1.000
hCs134_1 0.008 0.022 0.000 1.000
hBi214_1 -0.005 -0.038 -0.138 -0.572 1.000
hAnn_1 -0.000 -0.000 0.000 -0.021 0.011 1.000
hK40_1 -0.221 -0.027 -0.000 0.000 0.001 -0.000 1.000
hPb214_1 -0.273 0.000 -0.000 -0.028 0.016 0.001 -0.027 1.000
hPbx_1 0.097 -0.000 0.000 0.010 -0.006 -0.000 0.009 -0.354 1.000
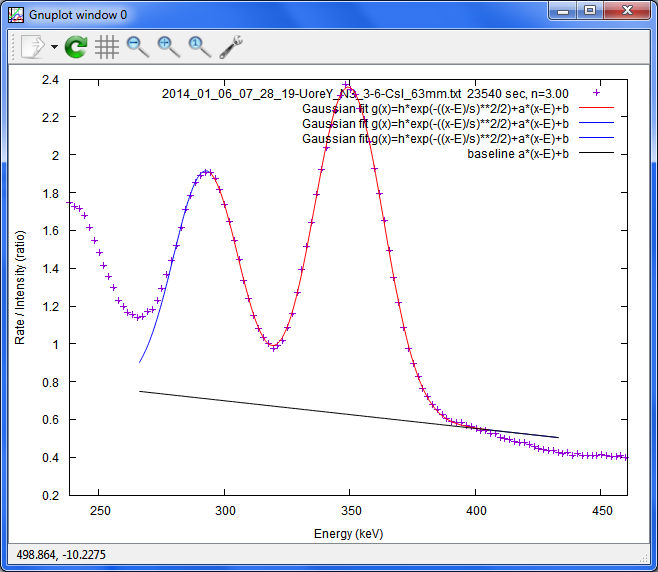
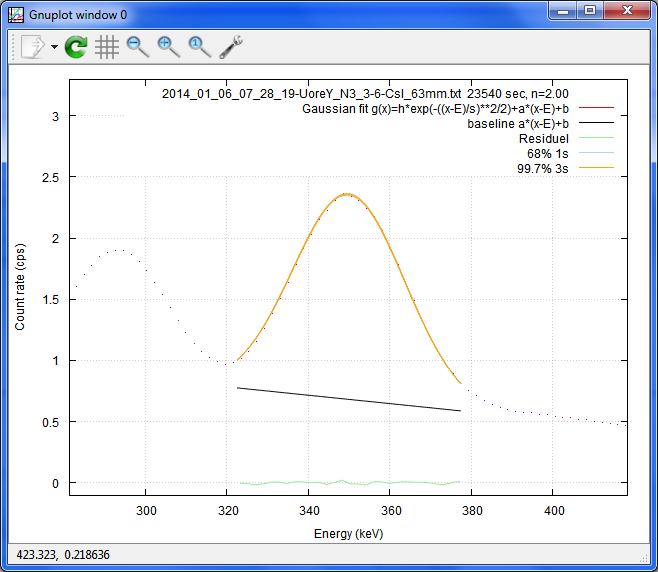
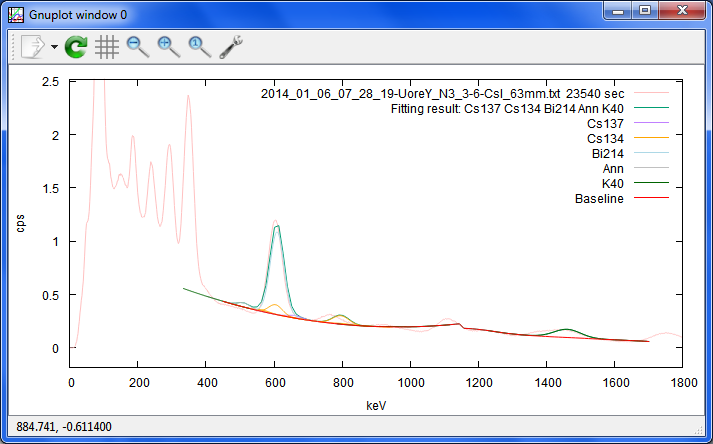
'2014_01_06_07_28_19-UoreY_N3_3-6-CsI_63mm.txt 23540 sec'
bb0=7.040185E-001, bb1=-3.378252E-004, bb2=-2.668545E-007, bb3=1.097549E-010 --- b0=9.852310E-002, b1=-1.839042E-004
Date: 2015/04/09 06:32(07) --- Name: nkom
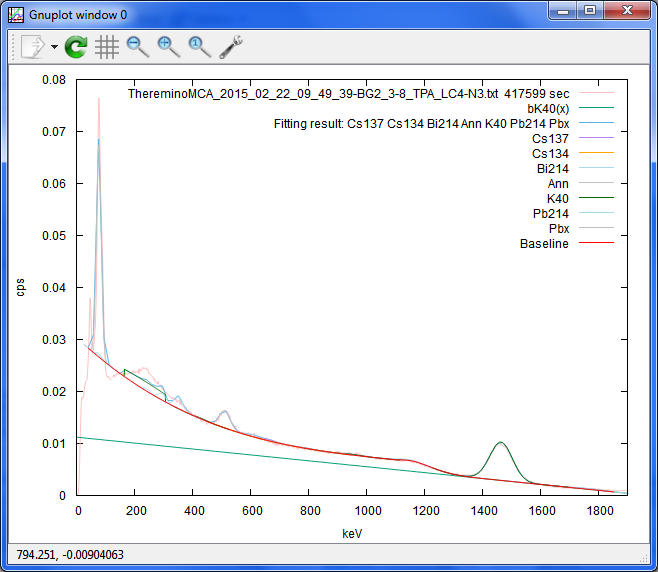
空マリネリのスペクトルだと、上手くいかないので、やはり400keV以下は、コンプトン丘の線を
そのまま使うのではなく、別の線にするか、加工しないと。
After 5 iterations the fit converged.
final sum of squares of residuals : 0.00120434
rel. change during last iteration : -7.39497e-006
degrees of freedom (FIT_NDF) : 868
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.00117792
variance of residuals (reduced chisquare) = WSSR/ndf : 1.38749e-006
Final set of parameters Asymptotic Standard Error
======================= ==========================
sK40_4 = 116.997 +/- 73.09 (62.47%)
eK40_1 = 1462.76 +/- 1.514 (0.1035%)
hCs137_1 = 0.000267016 +/- 0.0002792 (104.6%)
hCs134_1 = 2.28366e-005 +/- 0.0001979 (866.8%)
hBi214_1 = 0.000378162 +/- 0.0002931 (77.5%)
hAnn_1 = 0.00339672 +/- 0.0002992 (8.81%)
hK40_1 = 0.00737537 +/- 0.0002005 (2.718%)
hPb214_1 = 0.0024403 +/- 0.0003061 (12.54%)
hPbx_1 = 0.0407152 +/- 0.0004671 (1.147%)
correlation matrix of the fit parameters:
sK40_4 eK40_1 hCs137 hCs134 hBi214 hAnn_1 hK40_1 hPb214 hPbx_1
sK40_4 1.000
eK40_1 0.009 1.000
hCs137_1 0.000 0.007 1.000
hCs134_1 0.008 0.027 0.000 1.000
hBi214_1 -0.005 -0.048 -0.138 -0.573 1.000
hAnn_1 -0.000 -0.001 0.000 -0.021 0.011 1.000
hK40_1 -0.203 -0.045 -0.000 -0.001 0.002 -0.000 1.000
hPb214_1 -0.281 0.000 -0.000 -0.028 0.016 0.001 -0.024 1.000
hPbx_1 0.100 -0.000 0.000 0.010 -0.006 -0.000 0.008 -0.355 1.000
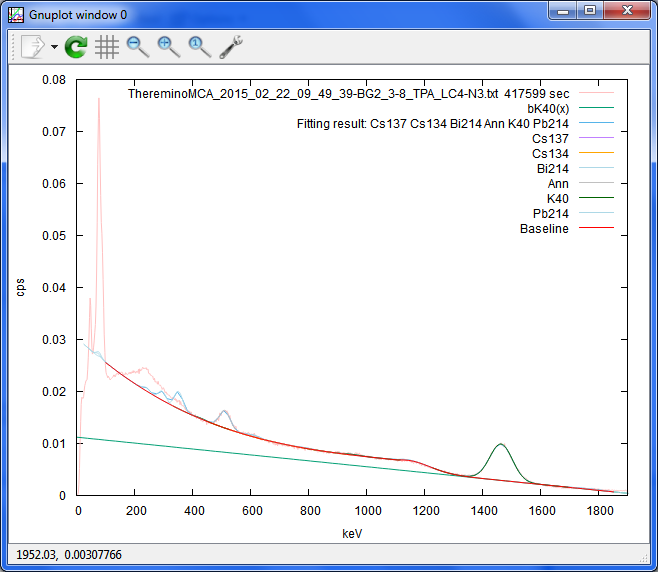
'ThereminoMCA_2015_02_22_09_49_39-BG2_3-8_TPA_LC4-N3.txt 417599 sec'
bb0=3.029613E-002, bb1=-5.202118E-005, bb2=4.143595E-008, bb3=-1.235081E-011 --- b0=2.805660E-003, b1=-5.685637E-006
Date: 2015/04/09 06:26(38) --- Name: nkom
バックスキャッターを入れてみたり、鉛のX線も追加してみました。
After 7 iterations the fit converged.
final sum of squares of residuals : 0.613772
rel. change during last iteration : -6.40497e-006
degrees of freedom (FIT_NDF) : 788
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.0279088
variance of residuals (reduced chisquare) = WSSR/ndf : 0.000778899
Final set of parameters Asymptotic Standard Error
======================= ==========================
sK40_4 = 41.4558 +/- 4.412 (10.64%)
eK40_1 = 1453.53 +/- 0.9656 (0.06643%)
hCs137_1 = 0.00147011 +/- 0.006914 (470.3%)
hCs134_1 = 0.00208444 +/- 0.004913 (235.7%)
hBi214_1 = 0.00706102 +/- 0.007287 (103.2%)
hAnn_1 = 0.00761008 +/- 0.007396 (97.19%)
hK40_1 = 0.291548 +/- 0.005036 (1.727%)
hPb214_1 = 0.00858512 +/- 0.00752 (87.59%)
hPbx_1 = 0.395691 +/- 0.01147 (2.9%)
correlation matrix of the fit parameters:
sK40_4 eK40_1 hCs137 hCs134 hBi214 hAnn_1 hK40_1 hPb214 hPbx_1
sK40_4 1.000
eK40_1 -0.001 1.000
hCs137_1 0.000 0.000 1.000
hCs134_1 0.008 0.002 0.001 1.000
hBi214_1 -0.004 -0.004 -0.138 -0.575 1.000
hAnn_1 -0.000 -0.000 0.000 -0.021 0.011 1.000
hK40_1 -0.137 0.010 0.000 0.000 -0.000 -0.000 1.000
hPb214_1 -0.278 -0.000 -0.000 -0.028 0.016 0.001 -0.015 1.000
hPbx_1 0.099 0.000 0.000 0.010 -0.006 -0.000 0.005 -0.355 1.000
bb0=2.359920E-001, bb1=-5.654531E-004, bb2=5.614934E-007, bb3=-1.605381E-010 --- b0=1.438051E-002, b1=-1.744667E-005
Date: 2015/04/08 12:34(34) --- Name: nkom
こっちは、バックグラウンドのスペクトル(遮蔽内の空マリネリ)。
誤検出は無し。
After 10 iterations the fit converged.
final sum of squares of residuals : 0.000575172
rel. change during last iteration : -5.27383e-006
degrees of freedom (FIT_NDF) : 840
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.000827483
variance of residuals (reduced chisquare) = WSSR/ndf : 6.84728e-007
Final set of parameters Asymptotic Standard Error
======================= ==========================
eK40_1 = 1462.9 +/- 1.119 (0.07649%)
hCs137_1 = 1.55883e-006 +/- 0.0001962 (1.258e+004%)
hCs134_1 = 3.59469e-006 +/- 0.0001391 (3868%)
hBi214_1 = 0.000336328 +/- 0.0002059 (61.22%)
hAnn_1 = 0.00339708 +/- 0.0002102 (6.188%)
hK40_1 = 0.00700646 +/- 0.0001441 (2.056%)
hPb214_1 = 0.00331679 +/- 0.0002057 (6.202%)
correlation matrix of the fit parameters:
eK40_1 hCs137 hCs134 hBi214 hAnn_1 hK40_1 hPb214
eK40_1 1.000
hCs137_1 0.007 1.000
hCs134_1 0.029 0.000 1.000
hBi214_1 -0.051 -0.138 -0.573 1.000
hAnn_1 -0.001 0.000 -0.021 0.011 1.000
hK40_1 -0.049 -0.000 -0.001 0.002 -0.000 1.000
hPb214_1 -0.001 -0.000 -0.027 0.015 0.001 0.000 1.00
3.51998011527975e-005, 2.03192988732844, -4.03042282340017
3.51998011527975e-005, 2.03192988732844, -4.03042282340017
Date: 2015/04/08 12:29(11) --- Name: nkom
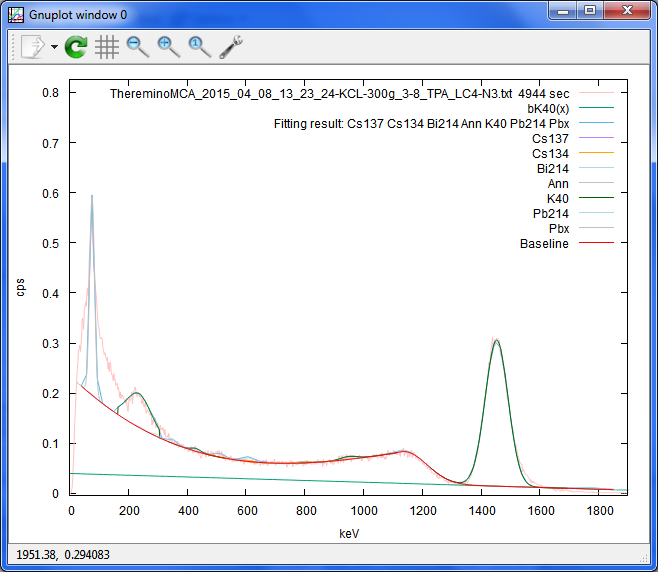
色々実験して、悩んだ結果、また少し幾つか学習し、若干気分がよくなりました。
低い方は、400keVまでは、まずまず。まだ、K40のピークの右側はあまり良くない。
400keV以下はどうするか、未定。
こんな感じで、線量の違うK40のスペクトルを幾つか取って、それでもって
パラメーターの動きがある場合に、それをどうモデル化するか考える予定。
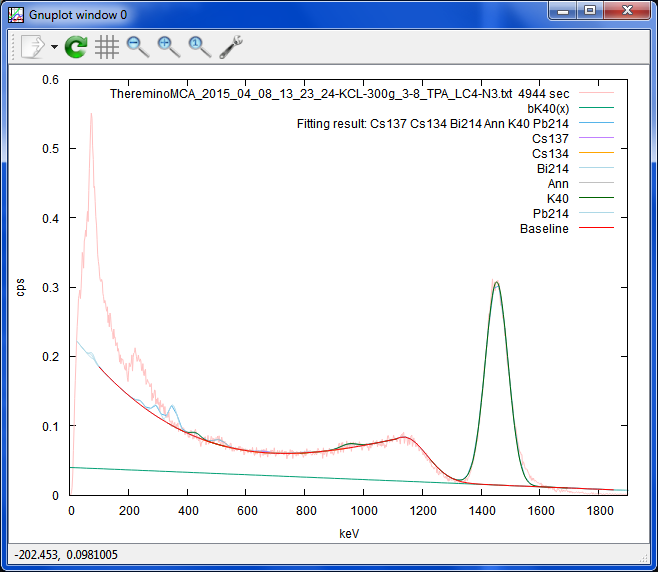
これは、KCL(No Salt)300g。何ベクレルK40が入っているのか、忘れましたが、
結構強いです。
After 27 iterations the fit converged.
final sum of squares of residuals : 0.419351
rel. change during last iteration : -9.94979e-006
degrees of freedom (FIT_NDF) : 763
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.0234437
variance of residuals (reduced chisquare) = WSSR/ndf : 0.000549608
Final set of parameters Asymptotic Standard Error
======================= ==========================
eK40_1 = 1453.53 +/- 0.807 (0.05552%)
hCs137_1 = 0.0018633 +/- 0.005808 (311.7%)
hCs134_1 = 6.52562e-006 +/- 0.004127 (6.324e+004%)
hBi214_1 = 0.000276706 +/- 0.006121 (2212%)
hAnn_1 = 0.00767282 +/- 0.006213 (80.98%)
hK40_1 = 0.293036 +/- 0.004306 (1.469%)
hPb214_1 = 0.0300514 +/- 0.006063 (20.17%)
correlation matrix of the fit parameters:
eK40_1 hCs137 hCs134 hBi214 hAnn_1 hK40_1 hPb214
eK40_1 1.000
hCs137_1 0.000 1.000
hCs134_1 0.002 0.001 1.000
hBi214_1 -0.004 -0.138 -0.575 1.000
hAnn_1 -0.000 0.000 -0.021 0.011 1.000
hK40_1 0.010 0.000 0.000 -0.000 -0.000 1.000
hPb214_1 -0.000 -0.000 -0.027 0.015 0.001 -0.000 1.000
0.000112799277905546, 2.1757777095367, -4.17763583245611
0.000112799277905546, 2.1757777095367, -4.17763583245611
Date: 2015/04/08 09:01(26) --- Name: nkom
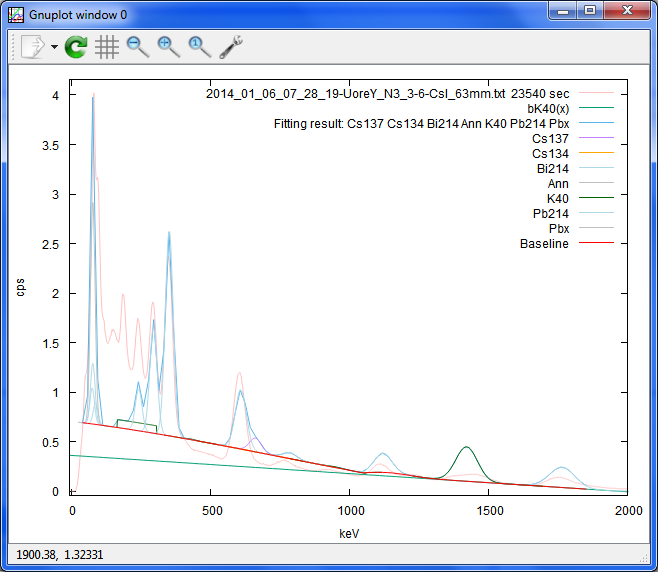
ウラン原石のスペクトルで下準備。Bi214は、当然ながら見つけていますが、ズレているのか
分解能が違うのか、ピークはあんまりぴったり合っていません。
あ、もしかしたら、横軸のパラメーターの名前と何かが被っていて、バグっているのかも。
それに、Cs134を「誤検出」している・・・
After 10 iterations the fit converged.
final sum of squares of residuals : 0.717617
rel. change during last iteration : -6.35822e-009
degrees of freedom (FIT_NDF) : 634
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.0336435
variance of residuals (reduced chisquare) = WSSR/ndf : 0.00113189
Final set of parameters Asymptotic Standard Error
======================= ==========================
b0 = 0.0963777 +/- 0.002397 (2.487%)
b1 = -0.000153961 +/- 1.278e-005 (8.304%)
cb0 = 9.09217e-007 +/- 5.725e-008 (6.296%)
cbx = 879.667 +/- 10.64 (1.209%)
cby = 0.0161896 +/- 0.007915 (48.89%)
hCs137_1 = 0.0231091 +/- 0.009238 (39.98%)
hCs134_1 = 0.0796018 +/- 0.007838 (9.846%)
hBi214_1 = 0.776726 +/- 0.01166 (1.501%)
hAnn_1 = 0.0400839 +/- 0.01153 (28.75%)
hK40_1 = 0.077133 +/- 0.006612 (8.572%)
correlation matrix of the fit parameters:
b0 b1 cb0 cbx cby hCs137 hCs134 hBi214 hAnn_1 hK40_1
b0 1.000
b1 0.249 1.000
cb0 -0.007 -0.002 1.000
cbx 0.166 0.661 -0.435 1.000
cby -0.064 0.864 -0.290 0.718 1.000
hCs137_1 -0.005 -0.001 0.232 -0.325 -0.174 1.000
hCs134_1 -0.007 -0.002 0.365 -0.337 -0.233 0.359 1.000
hBi214_1 0.004 0.001 -0.291 0.050 0.109 -0.201 -0.621 1.000
hAnn_1 -0.000 -0.000 -0.303 -0.213 -0.012 0.223 0.150 0.141 1.000
hK40_1 -0.512 -0.127 0.013 -0.087 0.025 0.010 0.014 -0.007 0.000 1.000
-1.09231479847223e-005, 9.09216854984459e-007, -13.3754051240426
-1.09231479847223e-005, 1, -13.3754051240426
'2014_01_06_07_28_19-UoreY_N3_3-6-CsI_63mm.txt 23540 sec'
Date: 2015/04/08 08:52(46) --- Name: nkom
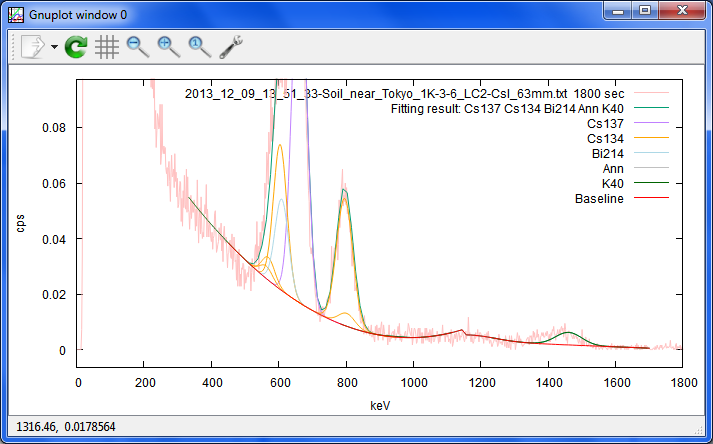
東京近郊のCs137が1000ベクレルくらい含まれる土のスペクトル。
これくらいだと、K40の左にサムピークとかの影響が出てきますし、Cs134やCs137の
コンプトン散乱も混ぜないと、駄目でしょう。
他に、なんとなく、ウラン系もBGよりはある様な気もします。
核種リストも追加しなきゃ。
After 23 iterations the fit converged.
final sum of squares of residuals : 0.0184206
rel. change during last iteration : -3.86034e-006
degrees of freedom (FIT_NDF) : 621
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.00544635
variance of residuals (reduced chisquare) = WSSR/ndf : 2.96628e-005
Final set of parameters Asymptotic Standard Error
======================= ==========================
b0 = 0.00166489 +/- 0.0003891 (23.37%)
b1 = -4.84898e-006 +/- 2.084e-006 (42.97%)
cb0 = 1.17501e-007 +/- 9.334e-009 (7.944%)
cbx = 968.454 +/- 17.68 (1.825%)
cby = 0.000285691 +/- 0.001094 (383.1%)
hCs137_1 = 0.131252 +/- 0.001525 (1.162%)
hCs134_1 = 0.0457712 +/- 0.0013 (2.841%)
hBi214_1 = 0.0329893 +/- 0.001926 (5.838%)
hAnn_1 = -5.48552e-005 +/- 0.001876 (3420%)
hK40_1 = 0.00453637 +/- 0.00107 (23.59%)
correlation matrix of the fit parameters:
b0 b1 cb0 cbx cby hCs137 hCs134 hBi214 hAnn_1 hK40_1
b0 1.000
b1 0.248 1.000
cb0 -0.007 -0.002 1.000
cbx 0.128 0.503 -0.731 1.000
cby -0.118 0.850 -0.170 0.497 1.000
hCs137_1 -0.005 -0.001 0.238 -0.342 -0.110 1.000
hCs134_1 -0.007 -0.002 0.368 -0.402 -0.168 0.359 1.000
hBi214_1 0.003 0.001 -0.288 0.154 0.098 -0.205 -0.626 1.000
hAnn_1 0.000 0.000 0.295 0.045 -0.019 -0.221 -0.151 -0.136 1.000
hK40_1 -0.514 -0.127 0.013 -0.072 0.052 0.009 0.013 -0.007 -0.001 1.000
-5.11729963059772e-006, 1.17501099066148e-007, -11.3133016340627
-5.11729963059772e-006, 1, -11.3133016340627
'2013_12_09_13_51_33-Soil_near_Tokyo_1K-3-6_LC2-CsI_63mm.txt 1800 sec'
Date: 2015/04/08 08:43(37) --- Name: nkom
テストしながら、細かいところも改良中。カウント数からcpsに変更したり、フィットした核種ごとに色を統一したりとか。
フィットの結果も当然cpsで出るので、(少なくとも私には)分かりやすいです。
既に、K40のコンプトンエッジの高さと、FWHMを一応固定(それぞれK40のピークの高さとエネルギーに依存)して、
あんまり変なことにならないか試しています。
After 14 iterations the fit converged.
final sum of squares of residuals : 0.000214352
rel. change during last iteration : -1.04765e-006
degrees of freedom (FIT_NDF) : 598
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.000598705
variance of residuals (reduced chisquare) = WSSR/ndf : 3.58448e-007
Final set of parameters Asymptotic Standard Error
======================= ==========================
b0 = 0.00283734 +/- 4.354e-005 (1.535%)
b1 = -5.33379e-006 +/- 2.171e-007 (4.071%)
cb0 = 2.24584e-008 +/- 1.201e-009 (5.348%)
cbx = 1147.39 +/- 20.43 (1.781%)
cby = 0.00212631 +/- 0.000144 (6.774%)
hCs137_1 = 0.0455306 +/- 0.0001716 (0.3768%)
hCs134_1 = 0.00702725 +/- 0.000146 (2.078%)
hBi214_1 = 0.0060446 +/- 0.0002142 (3.543%)
hAnn_1 = 0.000346262 +/- 0.0002119 (61.19%)
hK40_1 = 0.00794794 +/- 0.0001207 (1.518%)
correlation matrix of the fit parameters:
b0 b1 cb0 cbx cby hCs137 hCs134 hBi214 hAnn_1 hK40_1
b0 1.000
b1 0.339 1.000
cb0 -0.005 -0.002 1.000
cbx 0.084 0.238 -0.938 1.000
cby -0.140 0.370 0.715 -0.690 1.000
hCs137_1 -0.004 -0.002 0.277 -0.350 0.247 1.000
hCs134_1 -0.007 -0.002 0.398 -0.440 0.270 0.379 1.000
hBi214_1 0.003 0.001 -0.291 0.236 -0.115 -0.209 -0.622 1.000
hAnn_1 -0.000 -0.000 -0.285 0.122 -0.048 0.217 0.144 0.145 1.000
hK40_1 -0.510 -0.173 0.010 -0.049 0.069 0.009 0.013 -0.007 0.000 1.000
4.75998167916391e-005, 2.24584331708328e-008, -4.00447443141222
4.75998167916391e-005, 2.24584331708328e-008, -4.00447443141222
Date: 2015/04/08 06:38(05) --- Name: nkom
わかめのスペクトル。 ウラン系の609keV以外のピークや、トリウム系のピークを登録しないと、
良く合いません。でも、Cs137や134の誤検出はしていません。
After 69 iterations the fit converged.
final sum of squares of residuals : 3.62308e+006
rel. change during last iteration : -4.40905e-007
degrees of freedom (FIT_NDF) : 612
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 76.942
variance of residuals (reduced chisquare) = WSSR/ndf : 5920.07
Final set of parameters Asymptotic Standard Error
======================= ==========================
sEc = 90.2493 +/- 3.342 (3.703%)
b0 = 2386.28 +/- 54.72 (2.293%)
b1 = -1.14886 +/- 0.03615 (3.146%)
cb0 = 0.00351981 +/- 0.0001186 (3.369%)
cbx = 1037.86 +/- 11.13 (1.072%)
cby = 714.268 +/- 19.49 (2.728%)
hCs137_1 = 0.0111787 +/- 21.8 (1.95e+005%)
hBi214_1 = 273.765 +/- 27.1 (9.9%)
hCs134_1 = 3.17483 +/- 18.68 (588.3%)
hAnn_1 = 909.675 +/- 23.32 (2.563%)
hK40_1 = 1997.01 +/- 16.3 (0.8165%)
correlation matrix of the fit parameters:
sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
sEc 1.000
b0 -0.640 1.000
b1 0.573 -0.991 1.000
cb0 0.002 -0.001 0.000 1.000
cbx 0.263 -0.457 0.461 -0.841 1.000
cby 0.691 -0.898 0.857 0.102 0.247 1.000
hCs137_1 0.003 -0.001 0.001 0.378 -0.378 0.005 1.000
hBi214_1 -0.001 0.001 -0.000 -0.219 0.148 0.031 -0.238 1.000
hCs134_1 0.004 -0.002 0.001 0.468 -0.431 -0.023 0.363 -0.643 1.000
hAnn_1 0.002 -0.001 0.000 -0.021 -0.108 0.015 0.181 0.042 0.152 1.000
hK40_1 0.279 -0.121 0.048 0.007 0.016 0.241 0.012 -0.005 0.015 0.008 1.000
5.31998656822664e-005, 0.00351980678254175, -4.03371276210078
5.31998656822664e-005, 0.00417092803779983, -4.03371276210078
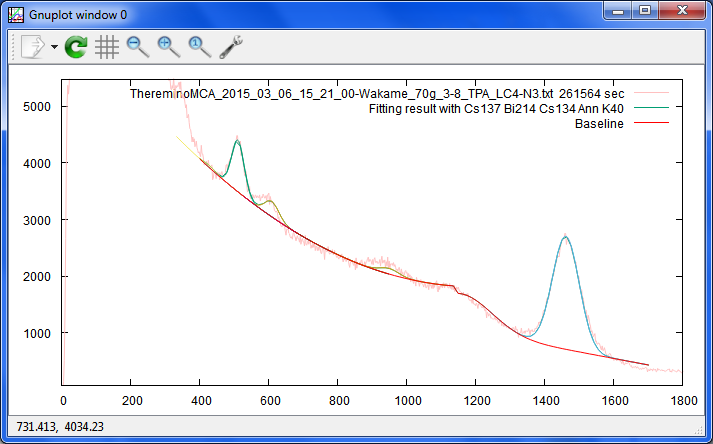
t 'ThereminoMCA_2015_03_06_15_21_00-Wakame_70g_3-8_TPA_LC4-N3.txt 261564 sec'
sEc = 90.2492623535012 sEc/sEc0 = 2.32464316217014
Date: 2015/04/08 06:05(51) --- Name: nkom
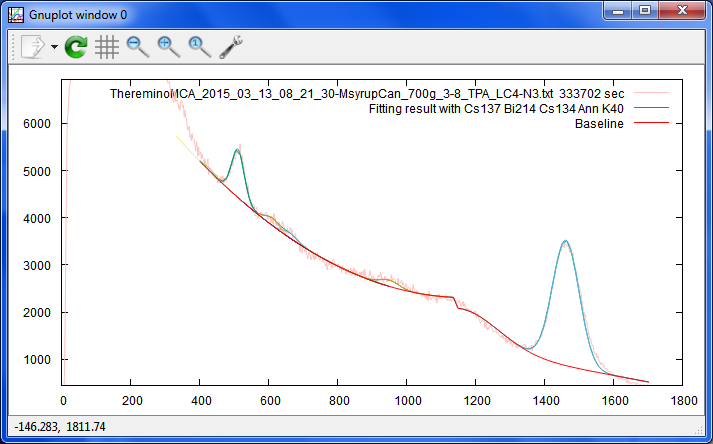
メープルシロップの缶、350mlの丸ごと測定は、このやり方でもCs137が見える様です。
After 19 iterations the fit converged.
final sum of squares of residuals : 4.28262e+006
rel. change during last iteration : -4.54858e-006
degrees of freedom (FIT_NDF) : 609
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 83.8583
variance of residuals (reduced chisquare) = WSSR/ndf : 7032.22
Final set of parameters Asymptotic Standard Error
======================= ==========================
sEc = 109.743 +/- 0.04094 (0.0373%)
b0 = 2859.79 +/- 45.46 (1.59%)
b1 = -1.37646 +/- 0.03205 (2.329%)
cb0 = 0.00488152 +/- 0.0001325 (2.714%)
cbx = 1028.9 +/- 8.438 (0.8201%)
cby = 961.675 +/- 15.43 (1.605%)
hCs137_1 = 103.548 +/- 23.92 (23.1%)
hBi214_1 = 154.134 +/- 29.65 (19.24%)
hCs134_1 = 1.83938 +/- 20.48 (1113%)
hAnn_1 = 1021.58 +/- 25.54 (2.5%)
hK40_1 = 2658.64 +/- 17.07 (0.6422%)
correlation matrix of the fit parameters:
sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
sEc 1.000
b0 -0.009 1.000
b1 0.008 -0.991 1.000
cb0 0.131 -0.001 0.000 1.000
cbx -0.137 -0.385 0.389 -0.872 1.000
cby 0.076 -0.827 0.785 0.116 0.115 1.000
hCs137_1 0.047 0.000 -0.001 0.383 -0.398 -0.007 1.000
hBi214_1 -0.011 -0.000 0.001 -0.218 0.152 0.049 -0.238 1.000
hCs134_1 0.047 0.001 -0.002 0.472 -0.450 -0.049 0.366 -0.643 1.000
hAnn_1 0.015 0.001 -0.001 -0.018 -0.117 0.016 0.182 0.042 0.153 1.000
hK40_1 -0.001 0.080 -0.145 0.007 -0.062 0.064 0.011 -0.004 0.014 0.008 1.000
3.75997849418451e-005, 0.00488151643360834, -4.05948345595782
3.75997849418451e-005, 0.00541404032505174, -4.05948345595782
t 'ThereminoMCA_2015_03_13_08_21_30-MsyrupCan_700g_3-8_TPA_LC4-N3.txt 333702 sec'
sEc = 109.743319339867 sEc/sEc0 = 2.82677165712455
Date: 2015/04/08 05:56(16) --- Name: nkom
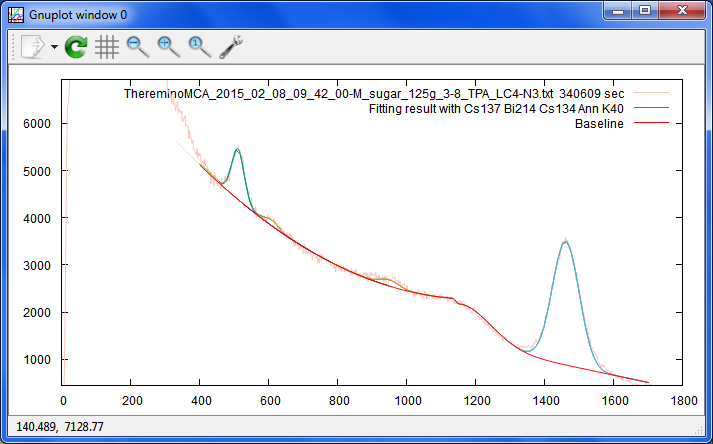
メープルシュガー125gのスペクトル。
やはり、こういうとても微妙なものは、BG差分じゃないと、難しい。
Cs137は、Gnuplotさんには、見えていない様です。
After 51 iterations the fit converged.
final sum of squares of residuals : 3.03693e+006
rel. change during last iteration : -9.74721e-006
degrees of freedom (FIT_NDF) : 627
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 69.5959
variance of residuals (reduced chisquare) = WSSR/ndf : 4843.6
Final set of parameters Asymptotic Standard Error
======================= ==========================
sEc = 87.5645 +/- 2.261 (2.582%)
b0 = 3126.03 +/- 48.83 (1.562%)
b1 = -1.53949 +/- 0.03226 (2.095%)
cb0 = 0.00445149 +/- 0.0001066 (2.394%)
cbx = 1027.45 +/- 7.693 (0.7487%)
cby = 860.853 +/- 17.59 (2.043%)
hCs137_1 = 0.0145174 +/- 19.53 (1.346e+005%)
hBi214_1 = 123.904 +/- 24.27 (19.59%)
hCs134_1 = 0.594409 +/- 16.73 (2814%)
hAnn_1 = 1072.27 +/- 20.9 (1.949%)
hK40_1 = 2629.53 +/- 14.63 (0.5562%)
correlation matrix of the fit parameters:
sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
sEc 1.000
b0 -0.643 1.000
b1 0.578 -0.991 1.000
cb0 0.002 -0.001 0.000 1.000
cbx 0.270 -0.466 0.471 -0.833 1.000
cby 0.695 -0.907 0.866 0.069 0.291 1.000
hCs137_1 0.003 -0.002 0.001 0.379 -0.378 -0.010 1.000
hBi214_1 -0.001 0.001 -0.000 -0.219 0.145 0.036 -0.237 1.000
hCs134_1 0.004 -0.002 0.001 0.469 -0.429 -0.039 0.363 -0.643 1.000
hAnn_1 0.002 -0.001 0.001 -0.021 -0.112 0.011 0.181 0.042 0.152 1.000
hK40_1 0.297 -0.135 0.061 0.007 0.023 0.252 0.012 -0.005 0.015 0.008 1.000
3.0400039859535e-005, 0.0044514876603354, -4.00880524094157
3.0400039859535e-005, 0.00519385358507668, -4.00880524094157
t 'ThereminoMCA_2015_02_08_09_42_00-M_sugar_125g_3-8_TPA_LC4-N3.txt 340609 sec'
sEc = 87.5644818781786 sEc/sEc0 = 2.25548850748232
Date: 2015/04/07 12:52(10) --- Name: nkom
こういう表示形式の切り替えとかも、簡単。
Date: 2015/04/07 12:44(48) --- Name: nkom
現在、これらのテストをするのに、必要な操作は二つだけ。
変数 f にスペクトルのファイル名を入れる。
@nl4 + エンターで、スクリプトを走らせる。
これで、後はスクリプトがファイルが新方式か、従来方式かを調べ、
測定時間を読み込み、スペクトルの幾つかの部分の統計を取って
下調べして、で、Fitとして結果を表示します。
後は、出てきたプロット画面で、Yのキーを押すと、縦軸のズーム。
Shift+Yで、ズームアウト。
同様に、Xで横軸のズーム。Shift+Xでズームアウト。
Lで対数(縦軸)とリニアの切り替え。
矢印キーでグラフの上下左右の移動。
で、マウスをグラフの上に乗せると、その地点のエネルギーと、カウント数が分かります。
K40の右側もあるし、ウラン系やトリウム系のテストもあるし、
あとどれくらいで出来るのやら。
ともかく、私が自分で使う分には、結構実用レベルに近づきつつあります。
この段階で(あんまり複雑になる前に)、パート4のページでも作って、
誰でも実験できるようにしましょうか。
で、テレミノMCAで読み込んで、テレミノ形式で保存すれば、
AT1320Aのスペクトルも、ベクモニのスペクトルも、EMF211も
KspectとかのSPE形式を使っている測定器も、これでFitできます。
まあ、Fitして曲線が出てくるだけで、定量的な推測をするには、
まだ手動で計算するか、スクリプトにちょっと追加する必要がありますが。
そういうのも徐々にくっつけていきます。
Date: 2015/04/07 12:31(53) --- Name: nkom
Sie氏方式で、コンプトンエッジの高さをK40のピークに連動させて固定させたら、
ちゃんとどれも収束するようになりました。
なので、3次式方式は、そのまま保存しておきますが、このまま色々と検討してみる予定。
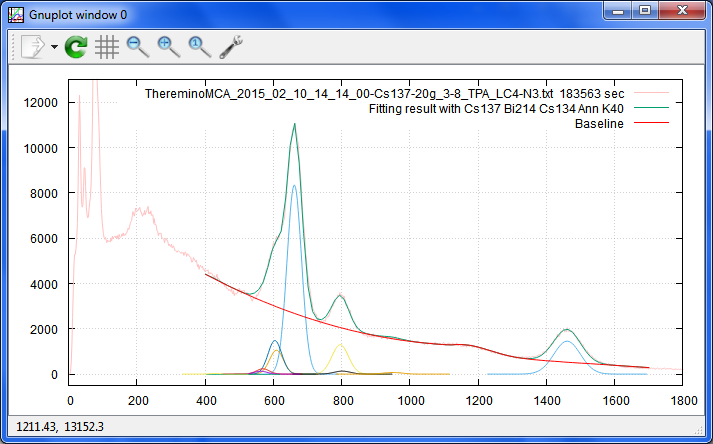
これは、汚染土壌20gを縦軸は対数目盛りでプロットしたもの。
コンプトン丘のところは、ほとんど直線・・・
After 27 iterations the fit converged.
final sum of squares of residuals : 7.9259e+006
rel. change during last iteration : -3.45391e-007
degrees of freedom (FIT_NDF) : 622
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 112.883
variance of residuals (reduced chisquare) = WSSR/ndf : 12742.6
Final set of parameters Asymptotic Standard Error
======================= ==========================
sEc = 77.4649 +/- 5.743 (7.414%)
b0 = 1985.69 +/- 72.5 (3.651%)
b1 = -0.999188 +/- 0.04857 (4.861%)
cb0 = 0.00497542 +/- 0.0001895 (3.809%)
cbx = 1096.16 +/- 14.5 (1.322%)
cby = 415.353 +/- 26.88 (6.472%)
hCs137_1 = 8348.51 +/- 32.13 (0.3848%)
hBi214_1 = 1056.43 +/- 39.46 (3.735%)
hCs134_1 = 1297.15 +/- 27.5 (2.12%)
hAnn_1 = 0.870107 +/- 33.98 (3905%)
hK40_1 = 1453.62 +/- 23.92 (1.646%)
correlation matrix of the fit parameters:
sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
sEc 1.000
b0 -0.608 1.000
b1 0.538 -0.990 1.000
cb0 0.001 -0.001 0.000 1.000
cbx 0.180 -0.333 0.337 -0.912 1.000
cby 0.572 -0.734 0.689 0.440 -0.247 1.000
hCs137_1 0.003 -0.001 0.000 0.405 -0.416 0.156 1.000
hBi214_1 -0.001 0.000 -0.000 -0.213 0.162 -0.020 -0.240 1.000
hCs134_1 0.004 -0.001 0.000 0.485 -0.468 0.140 0.378 -0.641 1.000
hAnn_1 0.003 -0.001 0.000 0.002 -0.105 0.059 0.187 0.040 0.158 1.000
hK40_1 0.309 -0.107 0.028 0.005 0.006 0.226 0.011 -0.004 0.014 0.008 1.000
4.75998167916391e-005, 0.00497541949346988, -4.00447443141222
4.75998167916391e-005, 0.000600841834503609, -4.00447443141222
Date: 2015/04/07 10:44(09) --- Name: nkom
ちょっと意外なことが分かりました。
測定開始から720秒後のスペクトルで試したら、Fitが収束しませんでした。
そこで、試しに、ベースラインを単純に3次式で誤魔化した、初期バージョンを走らせたら、
問題なく収束して、しかも、結果もなんか「それらしい」ものだったのです。
それじゃあ、Sie氏方式が失敗した、一番最初のは扱えるのだろうか?と思ってやってみたのがこれ。
なんと、収束しただけじゃなくて、最終の結果とまあまあ似たような線を引いているのです。
これ見たら、変に頑張って色々あわせようとするよりも、特にスペクトルのバラツキが
大きい段階では、単純なモデルの方が、良いのではないか?とか、そんな気がしてきたのです。
まあ、「三次式だけ」だと、コンプトンバレーとエッジの所が、ちょっと見苦しいので、
そこは、何か適当な曲線で足したり引いたりして、素人受けしやすいように
「見た目」も整えた方が良いのでしょうが、ギザギザグチャグチャなスペクトルしか
取れないような測定環境なら、それも関係ないかも、とか思ってしまいました。
まあ、Sie氏方式も、ちゃんと応答関数の形に整えて、K40のピークと
他の部分が連想するようになれば、多分収束もするし、最初から
それらしい線を出してくる可能性もありますが、両方のやり方を提供した方が良いのかも。
After 19 iterations the fit converged.
final sum of squares of residuals : 1299.28
rel. change during last iteration : -1.09504e-006
degrees of freedom (FIT_NDF) : 636
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 1.4293
variance of residuals (reduced chisquare) = WSSR/ndf : 2.04289
Final set of parameters Asymptotic Standard Error
======================= ==========================
ba = 1.5686e-005 +/- 4.181e-006 (26.65%)
bb = -0.0185114 +/- 0.003572 (19.3%)
bc = 8.59487 +/- 0.8547 (9.945%)
bd = -4.62597e-009 +/- 1.471e-009 (31.79%)
hCs137_1 = 0.36436 +/- 0.3959 (108.6%)
hBi214_1 = 0.500059 +/- 0.4933 (98.66%)
hCs134_1 = 0.000582708 +/- 0.329 (5.645e+004%)
hAnn_1 = 0.355194 +/- 0.4152 (116.9%)
hK40_1 = 0.966555 +/- 0.3225 (33.37%)
correlation matrix of the fit parameters:
ba bb bc bd hCs137 hBi214 hCs134 hAnn_1 hK40_1
ba 1.000
bb -0.991 1.000
bc 0.951 -0.980 1.000
bd -0.994 0.972 -0.918 1.000
hCs137_1 0.394 -0.400 0.362 -0.376 1.000
hBi214_1 -0.039 0.056 -0.069 0.024 -0.203 1.000
hCs134_1 0.405 -0.422 0.391 -0.377 0.312 -0.625 1.000
hAnn_1 0.330 -0.314 0.247 -0.329 0.212 -0.005 0.208 1.000
hK40_1 -0.005 0.031 -0.042 -0.038 -0.038 0.010 -0.043 -0.024 1.000
9.60117535958298e-006, 4.97350741027219e-006, -4.08646109812452
9.60117535958298e-006, 4.97350741027219e-006, -4.08646109812452
Date: 2015/04/07 10:22(03) --- Name: nkom
540秒で、Cs137もあるんじゃないか、と言い始めています。
After 16 iterations the fit converged.
final sum of squares of residuals : 2678.26
rel. change during last iteration : -4.2484e-006
degrees of freedom (FIT_NDF) : 608
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 2.09882
variance of residuals (reduced chisquare) = WSSR/ndf : 4.40504
Final set of parameters Asymptotic Standard Error
======================= ==========================
hEc = 0.625077 +/- 0.7198 (115.1%)
sEc = 68.4691 +/- 85.35 (124.7%)
b0 = 6.77181 +/- 2.616 (38.63%)
b1 = -0.00366451 +/- 0.00168 (45.83%)
cb0 = 4.6757e-006 +/- 3.382e-006 (72.34%)
cbx = 1184.8 +/- 364.3 (30.75%)
cby = 0.571182 +/- 0.8154 (142.8%)
hCs137_1 = 0.782375 +/- 0.601 (76.82%)
hBi214_1 = 0.706974 +/- 0.7435 (105.2%)
hCs134_1 = 0.017774 +/- 0.5143 (2894%)
hAnn_1 = 1.44734 +/- 0.6412 (44.3%)
hK40_1 = 4.34912 +/- 0.5102 (11.73%)
correlation matrix of the fit parameters:
hEc sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
hEc 1.000
sEc 0.437 1.000
b0 -0.832 -0.682 1.000
b1 0.817 0.657 -0.997 1.000
cb0 0.003 0.003 -0.003 0.003 1.000
cbx 0.400 0.321 -0.489 0.491 -0.851 1.000
cby 0.673 0.582 -0.772 0.755 0.521 -0.119 1.000
hCs137_1 0.006 0.006 -0.006 0.005 0.389 -0.367 0.207 1.000
hBi214_1 -0.002 -0.002 0.002 -0.002 -0.217 0.160 -0.063 -0.238 1.000
hCs134_1 0.008 0.008 -0.007 0.007 0.475 -0.424 0.218 0.369 -0.642 1.000
hAnn_1 0.004 0.004 -0.004 0.004 -0.013 -0.067 0.059 0.183 0.042 0.154 1.000
hK40_1 0.470 0.462 -0.460 0.418 0.007 0.200 0.452 0.013 -0.005 0.016 0.009 1.000
9.60117535958298e-006, 4.67570194529687e-006, -4.08646109812452
9.60117535958298e-006, 4.67570194529687e-006, -4.08646109812452
Date: 2015/04/07 10:15(23) --- Name: nkom
しかし、360秒で、K40を捕捉。511もBi214も、こんなもんじゃないでしょうか?と推測しています。
Cs137は、じぇんじぇん見えていません。
After 22 iterations the fit converged.
final sum of squares of residuals : 1768.4
rel. change during last iteration : -4.20916e-006
degrees of freedom (FIT_NDF) : 608
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 1.70545
variance of residuals (reduced chisquare) = WSSR/ndf : 2.90855
Final set of parameters Asymptotic Standard Error
======================= ==========================
hEc = 0.433227 +/- 0.7557 (174.4%)
sEc = 82.7853 +/- 128.8 (155.6%)
b0 = 4.72379 +/- 2.823 (59.76%)
b1 = -0.00258909 +/- 0.001781 (68.79%)
cb0 = 5.12856e-006 +/- 2.924e-006 (57.01%)
cbx = 1032.89 +/- 242.6 (23.49%)
cby = 0.34937 +/- 1.004 (287.4%)
hCs137_1 = -0.0453685 +/- 0.4925 (1086%)
hBi214_1 = 1.00132 +/- 0.6043 (60.35%)
hCs134_1 = 0.00697032 +/- 0.4212 (6043%)
hAnn_1 = 0.388911 +/- 0.5215 (134.1%)
hK40_1 = 2.62385 +/- 0.4703 (17.93%)
correlation matrix of the fit parameters:
hEc sEc b0 b1 cb0 cbx cby hCs137 hBi214 hCs134 hAnn_1 hK40_1
hEc 1.000
sEc 0.647 1.000
b0 -0.923 -0.772 1.000
b1 0.913 0.754 -0.998 1.000
cb0 0.003 0.003 -0.003 0.003 1.000
cbx 0.652 0.538 -0.713 0.714 -0.666 1.000
cby 0.918 0.787 -0.979 0.970 0.070 0.626 1.000
hCs137_1 -0.009 -0.008 0.008 -0.008 -0.406 0.307 -0.020 1.000
hBi214_1 -0.004 -0.003 0.004 -0.003 -0.213 0.111 0.008 0.240 1.000
hCs134_1 0.011 0.010 -0.011 0.010 0.485 -0.340 0.009 -0.379 -0.640 1.000
hAnn_1 0.007 0.006 -0.006 0.006 0.002 -0.089 0.016 -0.187 0.041 0.158 1.000
hK40_1 0.640 0.584 -0.617 0.587 0.006 0.417 0.654 -0.014 -0.006 0.018 0.010 1.000
9.60117535958298e-006, 5.12855965946958e-006, -4.08646109812452
9.60117535958298e-006, 5.12855965946958e-006, -4.08646109812452